10 – PRAYER TIMES
The hadith-i sherîf quoted in the books Muqaddimet-us-salât, at-Tefsîr-al-Mazharî and al-Halabî al-kabîr declares, “Jabrâîl ‘alaihis-salâm’ became my imâm by the side of the door of Ka’ba for two
days. We two performed the morning prayer as the fajr (morning
twilight) dawned, the early afternoon prayer as the
Sun departed from meridian, the late afternoon prayer when the shadows of
things became as long as their heights, the evening prayer as the Sun set [its
upper edge disappeared] and the night prayer when
the evening twilight darkened. In the second day, we performed the morning
prayer when the morning twilight matured, the early afternoon prayer as the
lengths of the shadows of things (rods) lengthened
by twice as much as their heights, the late afternoon prayer right after that,
the evening prayer when the fast was broken and the night prayer at the first
one-third of the night. Then he said ‘Oh Muhammad, these are the times of
prayers for you and the prophets before you. Let your Ummat perform each of these five
prayers between the two times at which we performed each’.” This
event took place on the fourteenth of July, one day after the Mi’râj and two
years before the Hegira. The Ka’ba was
It is fard (obligatory duty) for every Muslim male or female who are
’âqil and bâligh, that is, who are sane and pubert, that is, have reached the
age for marriage, to perform salât (prayer) five times a day in their correct
times. If a salât is performed before its due time, it will not be sahîh
(acceptable). In fact, it will be a grave sin. As it is fard to perform a salât
in its correct time for it to be acceptable, it is also fard to know with no
doubt that
---------------------------------
[1] It was (-3.56), i.e. the shadow pointed southwards, since the Sun's declination was ten minutes greater than the location's latitude, so culmination took place north of the observer's zenith.
you have performed it in its correct time. A
hadîth in the book Terghîb-us-salât declares,
“There is a beginning and an end of the time of
each salât.” The earth on which we live rotates around its axis in
space. Its axis is an imaginary straight line going through the earth’s center
and intersecting the earth’s surface at two symmetrical points. These two
points are termed the Poles. The sphere on whose inner surface the sun and the
stars are imagined to move is termed the celestial
sphere. Because the earth revolves around the sun, we get the
impression as if the sun were moving, although it is not the case. When we look
around, the earth and the sky appear to meet on the curved line of a tremendous
circle. This circle is termed the apparent horizon.
In the morning the sun rises on the eastern side of this horizon. It moves up
towards the middle of the sky. Reaching its zenith at noontime, it begins to
move down again. Finally, it sets at a point on the western end of the apparent
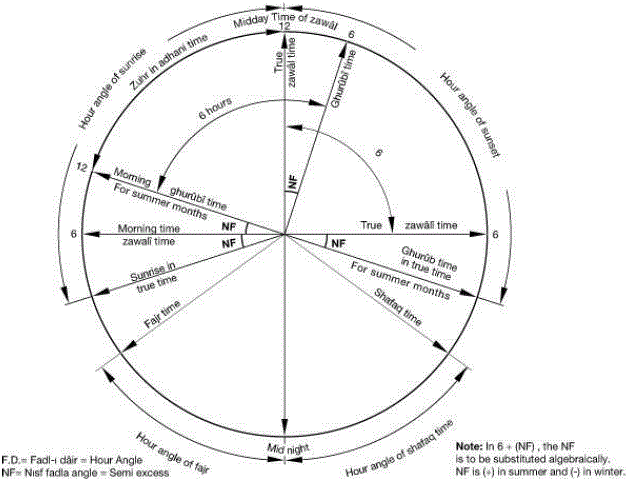
horizon. The highest point it reaches from the horizon is the time of noon (zawâl). At this time, the sun’s
altitude from the (apparent horizon) is termed the meridian
altitude (ghâya irtifâ’). A person who observes space is called observer (râsýd). The earth’s radius intersecting
the earth’s surface at a point exactly under the observer’s feet is at the same
time the observer’s plumb line. The observer is at point M, which is a certain
distance above the earth’s surface. ME is the observer’s plumb line. Planes
perpendicalar to this plumb line are termed the observer’s horizons.
There are six horizons: Please read the explanations below fig.1 A few pages ahead! 1– The plane MF, termed
(calculated horizon), which goes through the observer’s feet. 2– The plane BN,
termed (sensible horizon), which contacts the earth’s surface. 3– The plane LK,
termed (mer’î= valid, visible horizon), which is represented with a circle,
(circle LK), i.e. the (apparent horizon) surrounding the observer. 4– The
plane, termed (true horizon), which goes through the earth’s centre. 5– The
plane P, termed (canonical horizon), which goes through the apparent line of
horizon belonging to the highest point of the place where the observer is; the
circle q where this plane intersects the earth’s surface is termed (line of
canonical horizon). These five planes are parallel to one another. 6– The plane
of sensible horizon passing through the observer’s feet is termed the surface (sathî) horizon.
The higher the observer’s location, the wider and the
farther away from the sensible horizon is the
apparent horizon, and the closer is it to the true horizon. For this reason, a
city’s apparent prayer times may vary, depending on the altitudes of its
various parts. However, there is only one prayer time for each prayer of namâz.
Therefore, apparent horizons cannot be used for prayer times. Shar’î
(canonical) altitudes are used because they are dependent on the shar’î
(canonical) horizons, which do not vary with height. Each prayer of namâz has
three different prayer times for three of the six different horizons of every
location: True; apparent (zâhirî); and shar’î (canonical) times. Those who see
the sun and the horizon perform (each prayer of) namâz at its shar’î
(canonical) time, which is when the sun’s altitude from the shar’î horizon
attains its position prescribed for the prayer time. Those who do not see them
perform their prayers of namâz at their shar’î times determined by calculation.
However, altitudes based on shar’î (canonical) horizons are longer than apparent
altitudes based on apparent horizons. These horizons cannot be used because
prayer times are after noon. There are calculated and mer’î (observed, valid)
times for each of the aforesaid times of namâz. Calculated (riyâdî) times are
determined by calculation based on the sun’s altitude. Mer’î times are obtained
by adding eight (8) minutes and twenty (20) seconds to calculated times. For,
it takes the sun’s rays eight minutes and twenty seconds to come to the earth.
Or it is determined by observing that the sun has reached a certain altitude.
Namâz is not performed at calculated or true times. These times are used as a
means for determining the mer’î times. The sun’s altitude is zero at sunrise
and sunset. The altitudinal changes above the apparent horizon begin at sunrise
before noon, and they begin after true horizon after noon. Shar’î (canonical)
horizon is before true horizon before noon, and it follows true horizon after
noon. The sun’s altitude at the time of fajr-i-sâdiq (true dawn) is –19°
according to all four Madhhabs.[1] Its altitude to
initiate the time of night prayer is –19° according to Imâm-i-a’zam (Abû
Hanîfa, the leader of Hanafî Madhhab), and –17° according to the two Imâms
(Imâm Muhammad and Imâm Abû Yûsuf, two of Imâm-i-a’zam’s disciples), and
---------------------------------
[1] These four Madahhabs are Hanafî; Mâlikî; Shâfi’î; and Hanbalî.
according to the other
three Madhhabs. The altitude to indicate the beginning of early afternoon
prayer is the meridian altitude (ghâya irtifâ’), which, in its turn, is the
algebraic multiplication of the complement of latitudinal degrees and (the
sun’s) declination. Mer’î-haqîqî noon time
(zawâl) is when the center of the sun is observed to have reached the maximum
(meridian altitude) with respect to the true horizon. The altitudes for the
early and late afternoon (’asr) prayers change daily. These two altitudes are
determined daily. Since it is not always possible to determine (by observation)
the time when the edge of the Sun reaches the altitude from the apparent
horizon for a certain prayer, the books of fiqh explain the signs and indications
of this mer’î (valid) time (for each prayer). This means to say that the
apparent times of namâz are the mer’î times, not the calculated times. Those
who are able to see these indications in the sky may perform their daily
prayers at these apparent times. Those who are not able to see these
indications as well as those who prepare calendars, calculate the riyâdî times
when the edge of the Sun arrives at the relevant altitudes with respect to the
surface horizon in the afternoon. When the time clocks show these calculated
times, they perform their prayers within these mer’î
times.
By calculation, the riyâdî times when the sun reaches the prescribed
altitudes from the true horizon are determined. That the sun has reached this
mer’î time (or altitude) is observed eight minutes and twenty seconds after
this calculated time; this time (of observation) is called mer’î time. In other words, the mer’î time is
eight (8) minutes and twenty (20) seconds after the riyâdî time. Since the
beginning times whereto the time clocks are adjusted, i.e. the times of true
noon and adhânî sunset, are mer’î times, the riyâdî times indicated by the time
clocks are mer’î times. Although the riyâdî (calculated) times are written in
calendars, they change into mer’î times on the time clocks. For instance, if a
certain time found by calculation is, say, three hours and fifteen minutes,
this riyâdî three hours and fifteen minutes becomes a mer’î time of three hours
and fifteen minutes on the time clocks. First the haqîqî
riyâdî times, when the center of the sun reaches the altitudes
prescribed for the prayers of namâz from the true horizon, are found by
calculation. Then these times are converted into shar’î
riyâdî times by means of a process performed with the time called tamkîn. In other words, there is no need for also
adding 8 minutes and 20 seconds to the riyâdî times on the time clocks. The
difference of time between
true time and the shar’î time for a certain prayer
of namâz is termed the time of tamkîn. The time of tamkîn for each prayer time
is approximately the same.
In a location, the time for the morning
prayer begins, in all the four Madhhabs, at the end of canonical night, that is, with the sighting of the
whiteness called fajr sâdiq (true dawn)
at one of the points on the line of ufq-i zâhirî (apparent horizon) in the
east. This time is also the beginning of fast. The chief astronomer Ârif Bey
reports, “Since there are weak reports saying that the fajr sâdiq (true dawn)
begins when the whiteness spreads over the horizon and the altitude of the Sun
is -18° or even -16°, it is judicious and safe to perform the morning prayer 20
minutes later than the time shown on calendars.” The altitude (of the Sun) for
the fajr (morning twilight) is determined by observation of the line of
apparent horizon in a clear night sky by using our watch. Since times
corresponding to various altitudes are determined by calculation, the altitude
used in the calculation of the time complying with the observed time, is the
altitude for the fajr (dawn). The altitude of the shafaq (the disappearance of
the evening twilight) is determined with the same procedure. For centuries,
Islamic scholars have adopted the altitude for fajr as -19°, and have reported
that values other than this are not correct. According to Europeans, dawn
(fajr) is the spreading of the whiteness,[1] and the sun’s altitude is –18° at dawn. Muslims’
religious tutors are the Islamic scholars, and not the Christians or those
people who have not adapted themselves to any of the (four) Madhhabs. The time
of morning prayer ends at the end of zahirî night (solar
or apparent night), that is, when the
front [upper] edge of the Sun is seen to rise from the apparent horizon.
The celestial sphere, with the
earth at its centre like a point, is a large sphere on which all the stars are
projected. The prayer times are calculated by using the arcs of altitude, which are imagined to be on the
surface of this sphere. The two points at which the axis of the earth
intersects the celestial sphere are called the celestial
poles. The planes passing through the two poles are called the
planes of declination. The circles that these planes form on the celestial
sphere are called circles of declination. The planes containing the plumb-line
of a location are called the azimuth planes
(or vertical planes). The circles
---------------------------------
[1] This is the time when Astronomical twilight begins.
formed by the imagined intersection of planes
containing the plumb-line of a location and the celestial sphere are called the
azimuth or altitude
circles (or verticals). The
azimuth circles of a given location are perpendicular to the horizons of that
location. At a given location, there is one plane of declination and an
infinite number of azimuth circles. The plumb-line of a location and the axis
of the earth (may be assumed to) intersect at the centre of the earth. The
plane containing these two lines is both an azimuthal and a declination plane
of the location. This plane is called the meridian
plane of the location. The circle of intersection of this plane with
the celestial sphere is called the meridian circle
A location’s meridian plane is perpendicular to its plane of true horizon and
divides it by half. The line whereby it cuts through its plane of true horizon
is termed the meridian line of the location. The arc between the point of intersection
of the azimuth circle (vertical) passing through the Sun and true horizon and
the Sun’s centre is the arc of true altitude
of the Sun at a given location at a given time. The Sun crosses a different
azimuth circle every moment. The angles measured on an azimuth circle between
the point at which the circle is tangent to the Sun’s edge and the point at
which it intersects the sensible, apparent, mathematical and superficial
horizons are called the Sun’s apparent altitudes
with respect to these horizons. Its superficial altitude is greater than its
true altitude. The times when the Sun is an equal altitude from each of these
horizons are different. The true altitude is the angle between the two straight
lines projecting from the earth’s centre to the two ends of the arc of true
altitude in the sky. The angular measures of infinite number of circular arcs
of various lengths between these two half straight lines and parallel to this
arc are all the same and are all equal to the angle of true altitude. The two
straight lines that describe the other altitudes originate from the point where
the plumb line of the place of observation intersects the horizon. The plane
passing through the centre of the earth perpendicular to its axis is called the
equator plane. The circle of
intersection of the equatorial plane with the Globe is called the equator. The place and the direction of the equatorial
plane and those of the equator never change; they divide the earth into two
equal hemispheres. The angle measured on the circle of declination
between the Sun’s centre and the equator is called
the Sun’s declination. The whiteness
before the apparent sunrise on the line of apparent horizon begins two degrees
of altitude prior to the redness, that is, it begins when the Sun ascends to an
altitude of 19° below the apparent horizon. This is the fatwâ[1]. Non-mujtahids do not have the right to change
this fatwâ. It has been reported in Ibn ’Âbidîn (Radd-ul-muhtâr)
and in the calendar by M.Ârif bey that some ’ulamâ said that it began when the
Sun is a distance of 20° (from the apparent horizon). However, acts of worship
that are not performed in accordance with the fatwâ are not sahîh (acceptable).
The daily paths of the Sun are circles on the (imaginary inner surface
of the) celestial sphere and that are (approximately) parallel to one another
and to the equatorial plane. The planes of these circles are (approximately)
perpendicular to the earth’s axis and to the meridian plane, and intersect the
horizontal plane of a given location at an angle (which, in general is not a
right angle); that is, the daily path of the Sun does not (in general)
intersect the line of apparent horizon at right angles. The azimuth circle
through the Sun intersects the line of apparent horizon at right angle. When
the Sun’s centre is on the meridian circle of a location, the circle of
declination going through its center and the location’s azimuthal circle
coexist, and its altitude is at its daily maximum (from the true horizon).
The time of apparent zuhr, that is, the time of apparent early afternoon prayer is to be
used by those who can see the Sun. This mer’î time begins as the Sun’s rear
edge departs from the apparent zawâl or noon. The Sun rises from the
superficial horizon, that is, from the apparent horizon, which we, of a given
location. First, the time of apparent-mer’î zawâl begins
when the front edge of the Sun at its maximum altitude (from the superficial
horizon), that is, from the apparent horizon,
which we observe reaches the circle of the apparent zawâl position peculiar to
this altitude in the sky. This moment is determined when you no longer perceive
any decline in the length of the shadow of a pillar (erected vertically on a
---------------------------------
[1] Fatwâ is a conclusive explanation wherein an authorized Islamic scholar answers Muslims' questions. Conditions to be fulfilled to be an authorized Islamic scholar are explained in our publications, Belief and Islam, The Sunni Path, and Endless Bliss (chapter 33 of second fascicle and chapter 10 of third fascicle).
horizontal plane). Following this, the time of true-mer’î zawâl is when the centre of
the Sun is at the meridian [midday] of the location, that is, when it is at its
daily maximum altitude from the true horizon. Thereafter, when its rear edge
descends to its maximum on the western side of the superficial horizon of the
location, the time of apparent-mer’î zawâl
ends, the shadow begins to lengthen, and it is the beginning of the time of apparent-mer’î zuhr. The motion of the Sun and
the tip of the shadow are imperceptibly slow as it ascends from the apparent noon
time to true noon time, and as it descends thence to the end of the apparent
noon time, because the distance and the time involved are quite short. When the
rear edge descends to its maximum height on the western side of the superficial
horizon of the location, the time of apparent mer’î
zawâl ends and the time of canonical
mer’î zuhr begins. This time is later than the time of true zawâl by
a period of Tamkîn. For the difference
of time between the true and the canonical zawâls is equal to the difference of
time between the true and the canonical horizons, which in turn is equal to the
time of Tamkîn. The zâhirî (apparent)
times are determined with the shadow of the pillar. The canonical times (of the
prayers) are not found with the shadow of the pillar. The true time of noon is
found by calculation, time of Tamkîn is
added to this, hence the riyâdî (calculated) shar’î (canonical) time of zawâl
(noon). The result is recorded in calendars. The canonical time of zuhr
continues until the ’asr awwal, that is,
the time when the shadow of a vertical pillar on a level place becomes longer
than its shadow at the time of true zawâl by as much as its height, or until ’asr thânî, that is, until its shadow’s length
increases by twice its height. The former is according to the Two Imâms [Abû
Yûsuf and Muhammad ash-Shaybânî], and the latter is according to al-Imâm
al-a’zam.
Although the time of late afternoon prayer
begins at the end of the time of early afternoon prayer and continues until the
rear edge of the Sun is seen to set at the line of apparent horizon of the
observer’s location, it is harâm to postpone the prayer until the Sun goes
yellow, that is, until the distance between the Sun’s lower [front] edge and
the line of apparent horizon is a spear’s
length, which is five degrees (of angle). This is the third one of the daily three times of kerâhat (explained towards
the end of this chapter). Calendars in
The time of evening prayer begins when the Sun apparently sets, that is,
when its upper edge is seen to disappear at the line of apparent horizon of the
observer’s location. The canonical and the solar nights also begin at this
time. At locations where apparent sunrise and sunset cannot be seen, and in
calculations as well, the shar’î times are used. When the sunlight reaches on
the highest hill in the morning; it is the shar’î (canonical) time for sunrise.
And in the evening; when it is seen to disappear down the highest hill on the
western horizon, it is the mer’î shar’î time for sunset. The adhânî time clocks
are adjusted to twelve (12) o’clock at this moment. The time of evening prayer
continues until the time of night prayer. It is sunna to perform the evening
prayer within its early time. It is harâm to perform it in the time of ishtibâk-e nujûm, that is, when the number of
visible stars increase, that is, after the rear edge of the Sun has sunk down
to an altitude of 10° below the line of apparent horizon. For reasons such as
illness, travelling,[1] or in order to eat food that is ready, it might
be postponed until that time.
The time of night prayer begins, according to the Two Imâms,[2] with ’ishâi-awwal,
that is, when the redness on the line of
---------------------------------
[1] What
is meant by long-distance journeys, and also how a Muslim travelling a long
distance is to perform his daily prayers termed namâz (or salât), is explaned in full detail in the fifteenth chapter.
[2] 'Imâmeyn' means Two Imâm's'. In 'Fiqh', one of Islam's main scientific branches pertaining to acts of worship, 'Imâmeyn' means 'Imâm Muhammad and Imâm Yusûf, two of the highest disciples of
apparent horizon in the west disappears. The same
rule applies in the other three Madhhabs. According to Imâm-al-a’zam it begins
with ’ishâi-thânî, that is, after the
whiteness disappears. It ends at the end of canonical night, that is, with the
whiteness of fajri-sâdiq (true dawn) according to Hanafî Madhhab. The
disappearing of redness takes place when the upper edge of the Sun descends to
an altitude of 17° below the superficial horizon. After that, the whiteness
disappears when it descends to an altitude of 19°. According to some scholars
in the Shâfi’î Madhhab, the latest (âkhir) time for night prayer is until
canonical midnight. According to them, it is not permissible to postpone the
performance of night prayer beyond canonical midnight. And it is makrûh in the
Hanafî Madhhab. In the Mâlikî Madhhab, although it is sahîh (acceptable) to
perform it until the end of canonical night, it is sinful to postpone and
perform it after the initial one-third of the night. He who could not perform
the early afternoon and the evening prayers of a certain day in the times
prescribed by the Two Imâms must not postpone them to qadâ but must perform
them according to al-Imâm-al-a’zam’s prescription; in that case, he must not
perform the late afternoon and the night prayers of that day before the times
prescribed for these prayers by al-Imâm-al-a’zam. A prayer is accepted as to
have been performed in time if the initial takbîr is said before the end of the
prescribed time in Hanafî, and if one rak’a is completed in Mâlikî and Shâfi’î.
In his book A. Ziyâ Bey notes in his book ’Ilm-i
hey’et:.
---------------------------------
.Imâm a'zam Abû Hanîfa, the leader and founder of the Hanafî Madhhab, one of the only four valid Madhhabs in matters pertaining to Islamic practices; 'Tarafeyn' means 'Imâm a'zam Abû Hanîfa himself and his blessed disciple Imâm Muhammad'; and 'Shaikhayn' means 'Imâm a'zam himself and his blessed disciple Imâm Abû Yûsuf. In another register of Islamic nomenclature, e.g. when matters concerning the Sahâba (the blessed companions of Muhammad 'alaihis-salâm') are being dealt with, 'Shaikhayn' means 'Hadrat Abû Bakr as-Siddîq and Hadrat 'Umar ul-Fârûq'
“As one approaches the poles, the beginnings of the times for morning
and night prayers, i.e. the times morning and evening twilight, become farther
apart from the times of sunrise and sunset, respectively. Prayer times of a
location vary depending on its distance from the equator, i.e., its degree of
latitude, φ, as well as on the declination, δ , of the Sun, i.e., on months and days.” [At locations where latitude is greater than the complement of declination, days and nights do not take place. During the times when the sum of latitude and declination is 90°-19° = 71° or greater, that is, 90°-φ ≤ δ +19° or φ + δ ≥ 71°, for
example, during the summer months when the Sun’s declination is greater than
5°, fajr (dawn, morning twilight) begins before the shafaq (evening dusk,
evening twilight) disappears. So, for instance, in Paris where the latitude is
48°50', the times of night and morning prayers do not start during 12 to 30
June. In the Hanafî Madhhab, the time is the reason (sabab) for performing
prayer. If the reason is not present, the prayer does not become fard.
Therefore, these two prayers (salâts) do not become fard at such places.
However, according to some scholars, it is fard to perform these two salâts at
their times in nearby countries or places. [During the periods of time (12 to
30 June) when the times of these two prayers of namâz do not virtually begin,
it is better to (try and find the times that these two prayers were performed
on the last day of the period during which their prescribed times virtually
began and to) perform them at the same times].
The time of Duhâ (forenoon) begins when one-fourth of
nehâr-i-shar’î, i.e., the first quarter of the canonically prescribed duration
of day-time for fasting, is completed.
Half of the nehâr-i-shar’î is called the time of Dahwa-i-kubrâ. In adhânî time (reckoned from
sunset) dahwa-i-kubrâ=Fajr+(24-Fajr)÷2=Fajr+12-Fajr÷2=12+Fajr÷2. Hence, half
the time of Fajr gives the time of Dahwa-i-kubrâ reckoned from
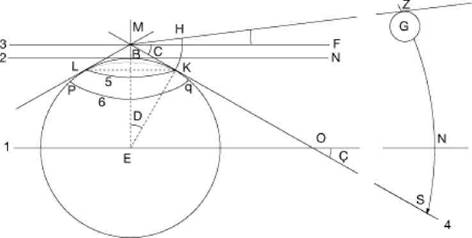
K![]() =
=![]() The point
at which the azimuthal plane through the Sun intersects the line of apparent
horizon.
The point
at which the azimuthal plane through the Sun intersects the line of apparent
horizon.
MS![]() =
=![]() The plane
of superficial horizon tangent to the Globe at point K, perpendicular to the
plumb-line at K.
The plane
of superficial horizon tangent to the Globe at point K, perpendicular to the
plumb-line at K.
HK![]() =
=![]() The
altitude of point K on the line of apparent horizon with reference to the
direction of the Sun, MZ. This is the altitude of the Sun with respect to the
line of apparent horizon. This altitude is equal to the altitude ZS of the Sun
with respect to the superficial horizon.
The
altitude of point K on the line of apparent horizon with reference to the
direction of the Sun, MZ. This is the altitude of the Sun with respect to the
line of apparent horizon. This altitude is equal to the altitude ZS of the Sun
with respect to the superficial horizon.
ZS![]() =
=![]() The arc of
azimuthal circle giving the altitude of the Sun with reference to the
superficial horizon. This angle is equal to the angle subtended by the arc HK.
The arc of
azimuthal circle giving the altitude of the Sun with reference to the
superficial horizon. This angle is equal to the angle subtended by the arc HK.
D=C=Ç=Angle of dip of horizon.
M![]() =
=![]() A high
place of the location.
A high
place of the location.
O![]() =
=![]() A point on
the straight line of intersection of true and superficial horizons.
A point on
the straight line of intersection of true and superficial horizons.
1![]() =
=![]() The plane
of true horizon 2.
The plane
of true horizon 2.
G![]() =
=![]() The Sun as
seen from the Earth.
The Sun as
seen from the Earth.
GA![]() =
=![]() The true
altitude of the Sun.
The true
altitude of the Sun.
B= The lowest place of the location.
words, it is equal to half the sum of times of
imsâk and iftâr in standard time
Since the amount of refraction of light by the atmospheric layers
increases as the Sun gets closer to the line of apparent horizon, it seems to
have risen on level places such as sea and planes when the upper edge of the
Sun is about 0.56° below the line of apparent horizon. And, in the evening its
disappearing below the horizon happens when the altitude of its upper edge goes
down to the same altitude after it sinks (below the apparent horizon).
Planes perpendicular to the plumbline of a
location, i.e., to the Earth’s radius through that location, are called the ufqs=horizons of the location. Only the
Ufq-i-sat-hî (superficial horizon) is an exception from this. Six types of
horizon may be defined. Ufq-i-haqîqî=True horizon
is the one passing through the Earth’s centre. Ufq-i-hissî=Sensible horizon is
the plane passing through the lowest point B of the location, that is, the
plane tangent to the Globe at point B. The angle formed at the Sun’s centre by
the two straight lines, one from the Earth’s centre and the other from the
Earth’s surface, is called the Sun’s ikhtilâf-i-manzar=parallax.
Its annual mean value is 8.8 seconds of angle. It is the difference between the
altitude of the centre of the Sun from the true horizon and the riyadî
(mathematical) or sensible horizon. Parallax results in a delay in the sighting
of rising of the Moon and the Sun. The horizontal plane passing through the
point M of a certain height where the observer is located is called the
observer’s ufq-i-riyâdî=mathematical horizon.
The khat ufq-i-zâhirî=line of apparent horizon
is the circle LK described as the line of tangency of the cone formed by the
revolution about the plumbline through M, of the line MK, projecting from the
observer’s eye at M and tangent to the Globe at K. The plane containing this
circle and perpendicular to the plumbline through M is called the ufq-i-mer’î=visible horizon of the observe the
surface of this cone is the ufq-i-sathî
(superficial horizon) (of the observer). The line of
apparent horizon appears to the observer, who stands at a certain
height, as a circular line along which the sky and the lowest points, such as
surfaces of seas and meadows, on the Earth’s surface intersect. This circular
line is formed by the points of intersection between the sensible horizon and
the earth’s surface. There is a plane of azimuth containing each point of this
circle. The plane of sensible horizon going through point K, which is
intersected
by the plane of azimuth containing the sun,
intersects the plane of azimuth at a right angle and along line MS. This
sensible horizon, plane MK, is called the ufq-i-sathî=superficial
horizon of the observer. There are
various superficial horizons for various altitudes at a location. The points K,
whereat they are tangent to the earth’s surface, make up the line of apparent
horizon. The direction of the ray projecting from the observer’s eye, i.e. the
line MS, is called the line of superficial horizon.
The vertical (azimuthal) arc, ZS, is the altitude of the Sun with respect to
the superficial horizon. The arc ZS is subtended by the angle inscribed between
the two straight lines projecting from the observer’s eye to the two ends of
this arc. As the Sun moves, the point of tangency K of the superficial horizon
MS moves on the line of apparent horizon and, thus, the plane of superficial
horizon changes momently. The observer will see the Sun when he looks at the
point H at which the straight line MZ from the observer to the Sun intersects
the arc HK, drawn parallel to ZS, the arc of altitude. He will perceive this
arc as the altitude of the Sun with respect to the line of apparent horizon.
The angle subtented by this arc HK is identical to that subtended by ZS, the
altitude of the rear edge of the Sun with reference to the superficial horizon.
Therefore, the apparent altitude HK is
used for the altitude with respect to the superficial horizon. The Sun sets
when it is at point S in the sky. The observer perceives as if it sets at point
K on the Earth. When the Sun and the stars go below the superficial horizon of
a location, i.e., when their altitude with reference to this horizon becomes
zero, the observers at every point on this horizon see them set. The observer
at point M sees the Sun setting at point K of the superficial horizon. In other
words, the time of sunset for the observer at point M is when the altitude of
the upper edge of the Sun attains zero with respect to the superficial horizon.
Similarly, the other prayer times of the observer are determined on the basis
of canonical altitudes with respect to the superficial horizons. Since the
canonical altitude of the Sun with respect to the superficial horizon is
perceived by the observer at point M as the altitude HK with respect to the
line of apparent horizon, the apparent altitudes
measured with reference to the apparent horizon are used for determining the
prayer times. The apparent altitudes are greater than those with respect to the
observer’s mathematical, sensible, visible and true horizons. The difference
between the altitude ZN with respect to the superficial horizon and the arc ZA
with respect to the true horizon true altitudes is called
the zâwiya inhitât-i
ufq=the angle of dip of horizon for the height of point M. The arc
of azimuthal circle equal to the angle of dip of horizon, i.e. the arc NS, is
the dip of horizon. Shar’î (canonical) times are
used in mountainous places where the apparent horizon cannot be seen.
The mathematical, sensible and visible horizons are identical for the
observer at the lowest point. He does not have (a separate) superficial
horizon. The line of apparent horizon is a small circle around this lowest
point B, and the altitude with respect to this line and the altitudes with
respect to all the other horizons are the same. The observer’s mathematical
horizon rises as the height of point of observation increases. His sensible horizon
becomes his superficial horizon. His line of apparent horizon descends towards
his true horizon and widens. Radius of each of such widening circles formed by
the descending lines of apparent horizon is an arc long enough to subtend angle
D, which in turn is equal to the angle of dip of horizon. The arc ZS, which
represents the Sun’s altitudes with respect to the superficial horizon, is
higher than the true altitude by the same length as the angle of dip of
horizon.
The sun’s reaching the time of noon with respect to this horizon means
any sort of reaching maximum horizon with respect to that horizon. When the
observer is at the lowest point its positions of zawâl with respect to all
horizons and to the line of apparent horizon coincide at one point, and the
day-time arc of the Sun’s daily path intersects the meridian at point A, –as is
seen on figures 1 and on a few pages ahead–, which is mid-point of its daily
path. This point is called the position of true zawâl. The apparent zawâl
positions for observers who are at higher places and who thereby see the sun,
with respect to the circles of apparent horizon peculiar to the heights they
occupy, are the circles of zawâl position which the points at maximum altitudes
form around the true zawâl in the sky. As the sun travels in its orbit, it
meets with each of these circles at two points. When it reaches the first
point, the time of apparent zawâl
begins. The end of the time of apparent zawâl is when the sun reaches the
second point. As the observer’s position becomes higher, dip of horizon takes
place and the circles of apparent horizon become larger. And so do these circles of zawâl position in the sky. Their radii
are equal to the
degrees of the arcs which are the radii of the
circles of apparent horizons of the earth. When the observer goes up to the
highest point of his location, the circle of zawâl position becomes the
greatest and the outermost. The arc between two points on this largest circle
of zawâl position is called the canonical zawâl position of the observer. The
superficial horizon of an observer at the highest point of a location is called
the ufq-i-shar’î=the canonical horizon of
the observer. The altitude of the Sun’s upper edge with respect to the
canonical horizon is called the shar’î irtifâ’=the
canonical altitude. The front edge of the Sun enters the circle of
canonical zawâl when its canonical altitude reaches its maximum with respect to
the canonical horizon pertaining to the place of sunrise. A hill so far from a
location as the shaded and the illuminated regions on it are not
distinguishable to the naked eye during the time of isfirâr (when the Sun’s
canonical altitude is less than 5° and it is yellow) is not considered to
belong to that location. The angle between the canonical and the true horizons
is equal to the angle of dip of an observer at the highest summit. The circles
of zawâl times are not visible; the Sun’s entering these circles and its going
out of them can be understood only from the shortening and elongation of the shadow
of a vertical rod erected on a level ground.
In the section on the mustahabs to be observed by a fasting Muslim in Radd al-muhtâr by Ibn ’Âbidîn and in the
annotation to Marâq al-falâh by at-Tahtâwî, it is noted, “One who is fasting and is
on a lower place, breaks his fast earlier than the one at a higher place when
and if he sees the sunset earlier. [In the Sharî’at, not the true times but the
apparent times are valid for those who can see the sun.] For those who are
unable to see the sunset, ‘sunset’ is when the hills in the east are left in
dark.” That is, it is the apparent sunset observed by those at the highest
place. In other words, it is the sunset down the canonical horizon. It is noted
also in the book Majma’al-anhur and the
Shafi’î book Al-anwâr li-a’mâlil abrâr that the canonical
sunset, which is determined by calculation, is to be taken into
account by those who are not able to see the sunset.
For easy determination of the times of early and late afternoon
prayers, ’Abd al-Haqq as-Sujâdilî, who was matured in the suhba of Muhammad
Ma’thûm al-Fârûqî as-Sirhindî, describes a method in his Persian book Masâ’il-i sharh-i Wiqâya,
printed in India in 1294 [1877 A.D.]:
“A circle is drawn on a level ground taking sunlight. This circle is
called the Dâ’ira-i Hindiyya=the Indian circle.
A straight rod, with a length equal to the radius of the circle, is erected at
the centre of the circle. The top end of the rod must be at an equal distance
from three different points on the circle to make it certain that it is
precisely vertical. This vertical rod is called the miqyâs=gnomon.
Its shadow extends beyond the circle on the western side before noon. As the
Sun moves higher up, that is, as its altitude increases, the shadow shortens. A
mark is made at the point where the tip of the shadow enters the circle.
Another mark is made at the point where the tip of the shadow exits on the
eastern side of the circle. A straight line is drawn from the centre of the
circle to the midpoint of the arc between the two marks. This straight line is
called the khat nisf-un-nahâr=the meridian line of
the location.” The meridian line extends in the north-south
direction. When the front edge of the Sun reaches its maximum altitude from the
line of apparent horizon of the location, the time of zâhirî zawâl=apparent noon begins. It is no
longer possible now to perceive the shortening of the shadow. Next, the centre
of the Sun comes to the meridian and is at its maximum altitude from the true
horizon. This is the time of haqîqî zawâl=true
noon. As it departs from this point, the shadow also departs from the meridian
line. The apparent zawâl time ends when the rear edge descends to its apparent
maximum altitude with reference to the sunset spot on the line of apparent
horizon. Now the time of apparent zuhr begins.
The shadow begins observably to lengthen. The middle of the time during which
the length of the shadow remains unchanged is the haqîqî
(true) zawâl time. As the sun passes the meridian, it is observed
with telescopes from London and thereby time clocks are adjusted in accordance
to hours reckoned from noon. At this mer’î haqîqî zawâl time, the true time is
twelve. The algebraic addition of this twelve to the equation of time[1] yields the meantime beginning,
i.e. the twelve, of
---------------------------------
[1] The
modification to be applied to apparent solar time, (i.e. the time as shown
on a sundial, which records the motions of the real (true) Sun across the sky,) to mean
solar time, (i.e. the time as shown on timepieces, with the irregularities
of apparent solar time, due to elliptic
movement of the Earth around the Sun, smoothed out). See Appendix IV.
the day on the local time clock. The riyâdî times
found by calculation also show the mer’î times on the time clocks. This mer’î zawâl time, which is the beginning for the
meantime clocks, is eight minutes and twenty seconds after the riyâdî zawâl time, which is the time when the sun
reaches the zawâl. The shortest length of the shadow, fay-i-zawâl varies with
latitude and declination.
A pair of compasses is opened by a length of fay-i-zawâl. The sharp
point of the compasses is placed at the point where the meridian line meets the
(Indian) circle and a second circle, whose radius is to the distance between
its centre and the point whereon it intersects the extension of the line of
meridian beyond the first circle, is drawn. It is the time of apparent ’asr awwal when the shadow of the gnomon
reaches the second circle. The second circle must be drawn anew daily.
Fay-i-zawâl is used only to find the times of early and late afternoon prayers.
It is not practicable in finding the times of other prayers.
It is written in the books Majma’al-anhur
and Riyâdh-un-nâsihîn: “The time of zuhr
begins when the Sun is at zawâl, that is, when rear side begins to descend from
the maximum altitude it has ascended from the line of apparent horizon. To
determine the time of zawâl, a rod is erected. It is the time of zawâl when the shortening of its shadow stops,
that is, when it does not shorten or lengthen. Performing salât at this time is
not permitted. The time of zawâl is completed when the shadow begins to lengthen.”
The maximum altitude mentioned in the book above is not the altitude with
respect to the true horizon. Two positions are noted: one is when the front
edge ascends to its maximum altitude from the superficial horizon, which is on
the eastern side of the line of apparent horizon; and the other is when the
rear edge descends to its maximum altitude from the superficial horizon, which
is on the western side of the line of apparent horizon. For, it is written in
the annotation to the book Imdâd that the
line of apparent horizon, not the true horizon, is to be taken into account in
determining the times (of prayers). The “time of apparent zawâl” commences when
the Sun’s front edge reaches its maximum altitude from the superficial horizon,
or from (the eastern side of) the line of apparent horizon. The time of
apparent zawâl ends when it
(the rear edge) begins to descend from its maximum
altitude from the superficial horizon with respect to the sunset position of
the line of apparent horizon. and the time of apparent zuhr commences. At this
moment the shadow of the gnomon is imperceptibly longer. The apparent time of
afternoon prayer (’asr) is when the length of this shadow increases by the
length of the gnomon. The period of time of true zawâl is a moment. However,
the period of time between the times of apparent zawâl of the front and the
rear edges is that between the times when the respective edges enter and exit
the circle on celestial sphere, which is called the circle of apparent zawâl
position and which centres round the point of true zawâl and and has a radius
equal to that corresponding to the angle of dip of the height at which the
observer is. The apparent zawâl position is not a point; it is an arc of circle
between two points whereat that circle, (which is called the circle of apparent
zawâl position,) intersects the Sun’s path. The largest of these circles is
(called) the circle of canonical zawâl position. In the Sharî’at, the zawâl
time, i.e. midday, is the period of time between the instants when the Sun’s
front edge enters this canonical circle and its rear edge exits. The time of canonical zawâl begins when the Sun’s
front edge enters the circle. The canonical zawâl time ends when the Sun’s rear
edge exits the circle, and the canonical zuhr time
begins. This time is determined by calculation and recorded in calendars.
The six-rak’at salât performed after the fard of evening salât is
called the salât of awwâbîn.
Defining and determining the times of various worships, that is,
comprehending and explaining them, require Islamic knowledge (’ulûm ad-dîn).
The ’ulamâ’ of fiqh wrote in their books
of fiqh the teachings which mujtahids (derived from the Qur’ân al-kerîm and hadîth-i-sherîfs
and) explained. It is permissible to calculate the prescribed times, (which
have been explained by mujtahids.) The times found out by calculation need to
be approved by the ’ulamâ’ of Islam. It is noted in the section on “facing the
Qiblâ in salât” in Radd al-muhtâr by Ibn
’Âbidîn, and in Fatâwâ-i Shams ad-dîn ar-Ramlî
that it is jâ’iz to determine the times of salât and direction of the Qibla by
calculation. It is noted in Mawdû’ât-ul-’ulûm:
“It is fard kifâya to calculate the prayer
times. It is fard for Muslims to know the
beginning and the end of the prayer times from the position of the Sun or from
the calendars approved by Islamic scholars.”
The Earth rotates about its axis from west to east. In other words, an
overhead view of it, like that of a globe placed on a table, would reveal that
it rotates in a counterclockwise direction. This is called the direct motion. The Sun and the fixed stars appear to
make a revolution per day from east to west. This is called the retrograde motion. The time between two
successive meridianal transits of a star in a certain location is defined as
one sidereal day. One-twenty-fourth of
this period is one sidereal hour. The
time interval between two successive transits of the centre of the Sun across
the meridian, that is, the time between successive instants of true zawâl is
called one true solar day. Meanwhile,
the Earth moves from west to east in the ecliptic plane and completes one
revolution per year around the Sun. Due to this motion of the Earth, the Sun
appears to move from west to east in the ecliptic plane, rotating about the
ecliptical axis through the Earth’s centre perpendicular to the ecliptic plane.
The average speed of this translational motion is about
axis of the Earth is inclined towards the Sun in the northern side of the ecliptic and more than half of the northern hemisphere takes sunlight. The declination of the Sun is about +23.5°. When the Earth arrives at a point about one-fourth of the length of its yearly route, the projection of axis of the Earth on the ecliptic deviates from the Sun-Earth direction by about 90°. At this time the Equinoctial line passes through the Sun. And the declination of the Sun is zero. When the Earth travels one-half of its yearly orbital route (from the point where it was on 22nd June), the perpendicular projection of the Earth’s axis on the ecliptic passes through the Sun again, but this time the northern hemisphere is pointing away from the Sun. The Sun is on the southern side of the Equator; less than half of the northern hemisphere and more than half of the southern hemisphere are exposed to sunlight; the Sun is 23.5° below the equator and hence declination of the Sun is -23.5°. When the Earth has travelled three-fourths of its yearly orbital route, that is, on 21st March, the Equinoctial line passes through the Sun and the Sun’s declination is again zero. Hasîb Bey notes in his book Kozmografya: “The light rays coming nearly parallel to one another are tangent to the Globe along a major circle. This major circle is called the dâira-i tanwîr=the circle of illumination. For the first six months during which the Sun is above on the northern side of the Equator, more than half of the northern hemisphere is on the side of the circle of illumination exposed to the Sun. The plane of illumination defined by this circle passes through the Earth’s centre, bisects the Globe and is perpendicular to the light rays from the Sun. Since the Earth’s axis is perpendicular to the equatorial plane, the angle of illumination between the line of illumination and the Earth’s axis is equal to the Sun’s declination. This is why there are days without nights and nights without daytime at places with latitudes greater than 90°-23°27'=66°33'. Let us assume a small circle sketched parallel to the circle of illumination 19° away from it on the unilluminated side. The phenomena of fajr (morning twilight, dawn, daybreak) and shafaq (evening dusk, evening twilight) take place within the zone between these two circles. At places where the complementaries to the latitudes are less than declination+19°, that is, at times when the sums of latitudes and declinations (φ + δ ) are greater than or equal to 90°-
19°=71°, the morning twilight or dawn begins
before the evening twilight disappears.” The Sun is in the south of the sky
when it is at meridian (at places where the Sun’s declination is smaller than
the latitudes). The observed paths of the Sun and the stars may be taken as
circles parallel to the Equator. The declination of the Sun is zero when the daily
path of the Sun coincides with the equatorial plane on the Gregorian March 21
and on September 23. On these two days, the durations of the night-time and
daytime are equal everywhere on the Earth. Since the nisf fadla (complement of
hour angle, semi excess daytime or night-time) is zero, the time of true zawâl
in ghurûbî time, and the times of true sunrise and sunset in true solar time
are all 06:00 hours everywhere. The canonical zuhr times in adhânî time are
also written as 6 o’clock in all authentic calendars, because approximately the
same amount of time of Tamkin for sunset exists in the time of zuhr, too.
During the days following these two days, the daily paths of the Sun gradually
depart from the Equator, and the Sun’s declination becomes +23°27' on June 22
and -23°27' on December 22. After these days[1], a gradual decrease starts in the absolute value
of the declination. During the time when the Sun is on the southern side of the
Equator, the major part of the northern hemisphere is on the dark side of the
circle of illumination, which is not exposed to the Sun. As the Earth rotates
about its own axis, the sunrise is observed when the front edge of the small
circle of apparent horizon of a location touches the illuminated hemisphere
borderlined by the circle of illumination. The Sun rises from the point of
exact east on the days when its declination is zero. As the declination
increases, the points of sunrise and sunset move towards the northern side of
the line of apparent horizon during summer and to its south in winter (on the
northern hemisphere). The arcs of line of apparent horizon (from the
equinoctial sunrise and sunset points), which change daily, are called the si’a=amplitudes of the Sun. In the countries in
the northern hemisphere (to the north of Tropic of Cancer), the Sun, after
rising appears to move and gain altitude towards south (of zenith or
plumbline).
---------------------------------
[1] The former is termed Summer Solstice, and the latter Winter
Solstice.
One-twenty-fourth of a true solar day is called
one true solar hour. The lengths of true
solar hours change daily. However, the units of time to be adopted for
measuring time by using clocks, that is, the lengths of days and hours, are
required to be the same every day. Therefore, the mean
solar day has been devised. One-twenty-fourth of a mean solar day is
called one mean hour. Ibn ’Âbidîn calls
the former mu’awwaj and the latter mu’tadil or falakî in
the chapter on menstruation. The length of one mean solar day is the average of
the lengths of true solar days in a year. Since there are 365.242216 true solar
days in a madârî (tropical) year, the [hypothetical] Mean Sun travels an
angular distance of 360° within this number of days and
-157
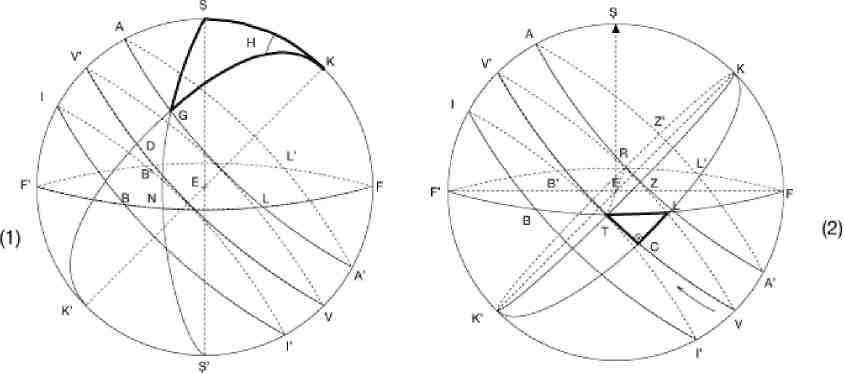
B = The point of sunrise on December 22.
T = The points of sunrise on March 21. and on
September 23.
L = The point of sunrise on June 22.
B' = The point of sunset on December 22.
R = The point of sunset on March 21. and September
23rd.
L' = The po int of sunset on June 22.
BI = Half of the daytime on December 22.
TV' = Half of the daytime on March 21 and
September 23.
LA = Half of the daytime on June 22.
AV' = CL = GD = Declination of the Sun on June 22.
IV' = Declination of the Sun on December 22.
VTV'R = The circle of equator in the sky.
AF', V'F', IF' = The maximum altitudes of the Sun.
A = The point of zawâl on June 22.
KLCK' = Semicircle of the declination on June 22.
GN = Angle of true altitude of the Sun.
KZK'Z' = The circle of declination on March 21,
and September 23.
TC = The arc of the equator equal to nisf fadla
during sunrise and sunset on June 22.
FK = F'K' = Arcs of polar altitude.
FK = ÞV' = Arc of latitude.
H = The angle of fadl-i dâ’ir, hour angle.
GA = Arc of fadl-i dâ’ir.
E = Observer’s location.
EÞ = Plumbine (direction to the sky).
TR = The East-West diameter of the circle of the
true horizon in the sky.
FEF' = The circle of meridian.
VKV'K' = The meridian circle.
F = Northern point of the true horizon.
ZL = The arc of Nisf fadla of Sunrise on June 22.
ZA = Z'A = The six-hour orbital travels on June
22.
Z'L' = The arc of Nisf fadla of Sunset on June 22.
LT, BT=Amplitudes of the Sun during sunrise.
it if - (negative). The variations in the Equation
of Time takes values between +22 seconds and -30 seconds of time per day as can
be seen in the table (or Equation of Time and Declination of the Sun) at the
end of this chapter.
Ahmed Ziyâ Bey states, “The value of the dip of horizon in angular
seconds is equal to the product of 106.92 and the square root of the altitude
in metres of the observer from the sensible horizon of the location.” Since the
highest hill near the observer in Istanbul is Çamlýca with a height of
is the Tamkin.” For instance, on March 21 and on
September 23, the angular altitude is 1°29'6.2" and the Tamkin, i.e., the
time taken by the edge of the Sun to descend that much altitude below the true
horizon along its trajectory, is 7 minutes 52.29 seconds (for Istanbul). Since
there are the variables of the declination of the Sun and the latitude of the
location in the formula of prayer times, period of Tamkin in a certain city
varies, depending on the degree of latitude and date. Although the period of
Tamkin for a city is not the same for every day or hour, there is a mean period
of Tamkin for each city. These Tamkin periods are given in a table at the end
of this chapter. As a precaution, 2 minutes is added to the Tamkin determined
by calculation, and the mean Tamkin for Istanbul is accepted to be 10 minutes
(of time). At any place with latitude less than 44°, the difference between
maximum and minimum tamkins in a year is about one or two minutes. A city has
only one tamkîn, which is utilized to find the canonical time of a certain
prayer of namâz from its true time. There are not different tamkîns for
different prayers of namâz. And there is no tamkîn in apparent times, either.
If a person, believing that the period of Tamkin is something added with
precautionary considerations, continues to eat for 3 to 4 minutes after the
imsâq (time to start fasting), his fast becomes fâsid (null) as are his fast
and evening prayer when he takes the sunset to be 3 to 4 minutes earlier, which
is written in the book Durr-i Yektâ, too.
The declination of the Sun, Tamkin and the Equation of Time change every moment
at a location, and the unit of haqîqî ghurubî (real sunset) time is slightly
different from the unit of true zawâl time, and therefore, the calculated
prayer times are not precisely exact. To be sure of the beginning of a prayer
time, 2 minutes of precaution is added to the period of Tamkin calculated.
There are three kinds of sunset: the first is the time when the true
altitude of the Sun’s centre is zero, called the true
sunset (haqîqî ghurûb); the second is the time when it is seen that
the apparent altitude of the Sun’s rear edge with respect to the apparent
horizon of the observer’s location is zero, that is, when its upper edge
disappears at the line of apparent horizon of the location, called the apparent sunset (zâhirî ghurûb); the third is the
time when the altitude of the rear edge relative to the canonical horizon is
calculated to be zero, called the canonical
sunset (shar’î ghurûb). There is only one canonical
horizon in a city. It is noted in all fiqh books that, of these three kinds of
sunset, the sighting of the apparent sunset is to be taken as basis. However
there are different lines of apparent horizons for different heights. Although
the sunset at the canonical horizon is the apparent sunset observed from the
highest hill (of the location), the times of this and true sunsets are always
determined by calculation. At the time of the calculated true sunset, the Sun
is seen to have not set yet at the lines of apparent horizons of high places.
This shows that the time for evening prayer and for breaking fast begins not at
the moments of the first and second types of sunset (as mentioned above) but at
a time later than that. First, the true sunset and then the apparent sunset,
and finally the canonical sunset take place. In the annotation of Marâq al-falâh, Tahtâwî
wrote: “Setting of the Sun means sighting of its upper edge disappear at the
line of apparent horizon, not at the true horizon.” The Sun’s setting at the
line of apparent horizon means its setting at the superficial horizon. If a
person, who has not been able to perform the late afternoon prayer, (performs
the evening prayer and breaks his fast and then) flies to the west by plane and
sees that the Sun has not set (yet at this place he has newly arrived at), he
performs the afternoon prayer and, after sunset, reperforms (i’âda) the evening
prayer and, after the ’Îd, makes qadâ of his fast.[1] In places where the
apparent sunset cannot be seen because of hills, high buildings and clouds, the
time of sunset, as stated in a hadîth, is the time of darkening of the hilltops
in the east. This hadîth sherîf shows that “in the calculation of the time of sunset or sunrise, not
the true or apparent altitudes but the canonical altitudes of the Sun relative
to canonical horizon are to be used,” that is, the Tamkin must be
taken into account. This hadîth should be followed, i.e., the Tamkin should be
taken into account in calculating the canonical times of all the other prayers,
too, because the true riyâdî times are determined by (a single-step
astronomical) calculation. There is a difference of a Tamkin between the true
and canonical times of a prayer. The Tamkin corresponding to the
---------------------------------
[1] In other words, he
reperforms that day's fast after the 'lyd of Ramadân. Please see the second
chapter of the fifth fascicle of Endless Bliss for Fasting in Ramadân
and 'lyd of Ramadân, or 'lyd of Fitra.
highest hill of a city
cannot be changed. If the Tamkin time is reduced, the late afternoon and the
following prayers, being performed before their prescribed time, and, by the same
token, the fasting being begun after the end of the sahur (imsâq), will not be
sahîh (valid). Up until the year 1982 no one had even considered re-arranging
the period of Tamkin in Turkey, and for centuries all the Scholars of Islam,
Awliyâ’, Shaikh al-Islâms, Muftîs and all Muslims had performed all their
prayers and started their fastings at their canonical times. (The calendar
prepared and published by the daily newspaper Türkiye gives the correct times
of prayers and fasting without making any alterations in the period of Tamkin.)[1]
For the calculation of early time for any salât in accordance with the
canonical horizon, the altitude of the Sun specific to this salât must be
known. First, the true solar time indicating the difference between midday or
midnight and the time when [the center of] the Sun reaches the altitude for the
salât with respect to the true horizon on its path at a location of a certain
latitude on a given day with a certain declination of the Sun’s center, is
calculated. This time is called fadl-i dâir =
hour angle. To determine the true altitude specific to a salât, the altitude of
the Sun’s upper edge with respect to the mathematical horizon is measured with
the help of a quadrant (rub’-i-dâira or
astrolabe) at the moment when the prayer time written in fiqh books begins.
From this, the true altitude can be calculated. [The apparent altitude is
measured with respect to the apparent horizon by using the sextant.] In the
astronomical triangle[2] KÞG, the arc KG is one side, GD is the complement
of declination, the arc KÞ is one of the sides, KF is the complement of the
altitude of the pole or complement of the location’s latitude, and the arc ÞG
is the complement of the true altitude GN (Figure 1 on page 142). The angle H
at the polar point K of the triangle, or the degree of the arc GA opposite this
angle, represents fadl-i dâir (hour angle); this is calculated in degrees of
arc, and its multiplication by four produces the true time in minutes. The
amount of the time of hour
---------------------------------
[1] Please
visit the websites: "http://www.turktakvim.com" and "http://www.namazvakti.com" and
"www.islamicalendar.co.uk".
[2] Vertices of this triangle are the Sun (G), the observer's zenith (S), and the celestial north pole (K).
angle is combined with the time of true or ghurûbî
zawâl or midnight, thus the true prayer time
is obtained in true zawâlî or ghurûbî time. Then the ghurûbî time is converted
into adhânî by adding one unit of Tamkin to it. The zawâlî time is converted
into mean time by adding the equation of time to it. Then the Shar’î (canonical) time
of the salât is obtained from these adhânî and wasatî (mean) ghurûbî times.
While doing this, the time of tamkîn,
which is the period between the time when the edge of the sun has reached the
altitude peculiar to this namâz from the canonical horizon and the time when
the edge of the sun has reached this altitude from the true horizon, is taken
into consideration. For the difference of time between the true and canonical
times of a namâz is equal to the difference of time between the true horizon
and the canonical horizon. And this difference, in its turn, is called the time
of Tamkîn. The canonical times are found by subtracting one unit of Tamkin from
the calculated true prayer times before midday, which is a period wherein the
Sun traverses the canonical horizon before traversing the true horizon.
Examples of this are the times of imsâk and sunrise. Ahmad Ziya Bey and Kadûsî
say in their books Rub-i-dâira, “Fajr
begins when the upper edge of the Sun has reached a position 19° below the
canonical horizon. The canonical time of imsâk with respect to true time is
obtained by subtracting Tamkin from the calculated true time of fajr (dawn).”
Hasan Shawki Efendi, senior professor of Islamic sciences at the Fâtih Madrasa
who translated Kadûsî’s Ýrtifâ’ risâlesi,
describes the method of finding the time of imsâk in its ninth chapter and
comments: “The times of true imsâk we have obtained by calculation are without
Tamkin. A person who will fast must stop eating 15 minutes, i.e. two units of
Tamkin, before this time. Thus, he protects his fast from being fâsid.” As it
is seen, to find the canonical adhânî time of imsâk, he is also subtracting
twice the Tamkin from the true ghurûbî time, and he reports that otherwise the
fasting will be nullified. [One unit of Tamkin is subtracted from the ghurûbî
time for finding the Shar’î time, and another unit of Tamkin is subtracted from
the ghurûbî time for converting it to the adhânî time.] We have observed that,
in the determination of true fajr and sunrise in adhânî time, twice the period
of Tamkin was subtracted in the tables of canonical times for Erzurum by hadrat
Ibrâhîm Haqqî and also in the book Hey’et-e felekiyya by Mustafa Hilmî efendi
in 1307.
The same is written in the book Hidâyat-ul-mubtadî fî ma’rifat-il-awqât bi-rub’i-d-dâira
by ’Ali bin ’Uthmân; he passed away in 801 [1398 A.D.]. On the other hand, to
find the canonical prayer times within the period after midday, wherein the Sun
transits the canonical horizon after transiting the true horizon, one unit of
Tamkin is added to the true times. Prayer times in this category are early and
late are afternoon, evening, ishtibâk and night. Ahmed Ziyâ Bey states as
follows in the same book, in the chapter dealing with the time of Zuhr: “If
Tamkin is added to the time of true zawâl in mean time, the time sahr’î
(canonical) Zuhr in mean time is obtained.” Always one unit of Tamkin is
subtracted to convert a prayer time known in terms of ghurûbî horizons within
the period covering noontime and teherafter to the shar’î (canonical) time with
respect to the canonical horizons, one unit of Tamkin is added. Then one unit
of Tamkin is subtracted to convert it to the adhânî time. Consequently, the
adhânî times of these these salâts are the same as their ghurûbî times. The
shar’î (canonical) times determined with respect to haqîqî (true) or ghurûbî
times are converted to the wasatî (mean) and adhânî times and written on
calendars. The riyâdî times, which are calculated in terms of riyâdî time
system, also indicate the mer’î times on time clocks.
NOTE: To determine the zuhr
time in adhânî true time from the ghurûbî true zawâl time, the Islamic scholars
subtracted the Tamkin at ghurûb from it, and they obtained the ghurûbî zawâl
time again by adding the period of Tamkin, which is the method for finding the
shar’î time at zawâl. This shows that the Tamkin at at the time of zuhr must be
equal to the difference of time between the true and canonical horizons, i.e.,
to the Tamkin at sunset. Likewise, tamkins for all the shar’î prayer times are
equal to those at sunrise and sunset. The book al-Hadâiq
al-wardiyya says, “Ibni Shâtir ’Ali bin Ibrâhîm [d. 777 (
Kashf-ul-qinâ’ ’an ma’rifat-il-waqt
min al-irtifâ’.”
It is seen in the calendar ’Ilmiyye
sâlnâmesi prepared by Mashîhat-i
Islâmiyya, the-highest council of the Ottoman ’ulamâ’, for the year
1334 [1916 A.D.] and in Türkiye’ye Mahsûs Evkat-ý
Þer’iyye book no. 14 published by the Kandilli Observatory of the
University of Istanbul in 1958 that Tamkin was taken into account in the
calculations of the canonical times of prayers. We have seen that the times
determined as a result of the observations and calculations carried on by our staff,
composed of true men of Islam and specialized astronomers using latest
instruments, are the same as those found and reported by Islamic scholars, who
used the rub-i-daira=astrolabe, for
centuries. Therefore, it is not permissible to change the quantities of Tamkin,
which means to defile the prayer times.
One mean solar day on the time clocks is twenty-four hours. A period of
twenty-four hours which begins when a time measuring instrument, e.g. our
watch, shows twelve o’clock at the haqîqî zawâl time and ends at twelve o’clock
the following day is called the mean solar day.
The lengths of mean solar days are all equal. On the other hand, the duration
of time that begins when our watch shows twelve at the time of zawâl and ends
at the time of zawâl the following day is called the true solar day. The length of a true
solar day, which is the time taken by the center of the Sun between
two successive zawâl times,[1] is equal to the length
of a mean day four times in a year. Except on these days, their daily lengths
differ by the amount of daily variation in ta’dîl-i zamân (Equation of Time).
The length of a ghurûbî (of sunset) day is the time between two successive
settings of the center of the Sun at the true horizon. An adhânî (of the adhân) day
is the time between two successive canonical settings of the upper [rear] edge
of the Sun at the canonical horizon of a location. When one of these settings
is observed, the adhânî clock is adjusted to 12. Though an adhanî day is equal
in length to a ghurûbî day, the former begins a period of Tamkin later than the
latter. Since the Sun’s ascent to the meridian and its descent thence take
place only once in a ghurûbî day versus its ascent to and descent from two
different altitudes in a true zawâlî day, there is one-or-two-minutes
difference of length between these two-days. Though
---------------------------------
[1] When a calestial object is
on the obzerver’s meridian, it is at culmination or in transit.
this variation results
in a difference of seconds between the hour units of the true and ghurûbî
times, this difference is neutralized with precautionary modifications made in
Tamkin. Time clocks indicate the adhânî or wasatî (mean) times, not the haqîqî
(true) or ghurûbî times. Let us set our clock (calibrated to run at the rate of
mean time) to 12:00 o’clock at the time of canonical sunset on any day. The
next day, the time of setting of the rear edge of the Sun at the canonical
horizon will differ by a little less than one minute from mean solar day, i.e.,
24 hours. This difference, which develops between the lengths of the following
haqîqî (true) and wasatî (mean) days which are originally equal, is termed equation of time.[1]
Lengths of nights and days have nothing to do with equation of time; nor do
ghurûbî or adhânî times. Lengths of days and hours in adhânî hours are equal to
lengths of true solar days and hours. For this reason, when time clocks are
adjusted to 12 at the time of sunset daily, they indicate the length of true
day, not the length of mean day.
The clocks set to keep the adhânî time must be adjusted to 12:00 at the
time of canonical sunset calculated in mean solar time every evening. Every
day, these clocks must be advanced as the time of sunset retards and taken
backwards as it advances. There is a mean length for an adhânî day, nor an
equation of time. It is written in the calendar Mi’yâr-i
awqât prepared in Erzurum in the Hijrî Qamarî year
---------------------------------
[1] The dates on which the
true and mean solar times are equalized, i.e. when the difference
between them is zero, are April 15, June 14, September
1, and December 25. Please see Appendix IV.
Qibla.” The adhânî clock is not adjusted on the
days on which the total variation of the time of sunset is less than 1 minute.
In Istanbul, they are moved 186 minutes forward in 6 months, and 186 minutes
backward in the following 6 months. These clocks adjusted as above measure time
in reference to the beginning of the adhânî day. Calculation of times of salât,
however, is done in reference to the time the ghurûbî day begins. Since an
adhânî day begins one unit of Tamkin later than a ghurûbî day, times of salât
are converted into riyâdî adhânî time by subtracting the Tamkin from the
ghurûbî times determined by calculation. Equation of time is not useed in
calculating the ghurûbî or adhânî times.
Since the Earth rotates round its axis from west to east, the places to
the east see the Sun before those to the west. Prayer times are earlier in the
east. There are (360° of) imaginary meridian semicircles running between the
two poles, and the semicircle passing through London (Greenwich) has been
accepted as the one for reference. The is one degree of angular distance
between two successive semicircles. As the Earth rotates, a city goes 15°
eastward in one hour. Therefore, of two cities one degree of longitude apart
from each other but with the same latitude, prayer times for the one on the
east are four minutes earlier. In places on the same meridian, that is, with
the same longitude, the time of zuhr and true zawâl (midday) are the same. The
times of zawâl and zuhr on the basis of ghurûbî time and other prayer times
differ from each other depending on their latitudes. As the latitude increases
the times of sunrise and sunset become farther away from the time of noon towards
summer and vice versa in winter. A quantity is measured in reference to a
certain beginning; e.g. zero. The one more distant from zero is said to be
more. For starting the clocks from zero they are either adjusted to zero or to
12 (or 24). The moment at which certain work is started is said to be the time of that work. The time may mean a moment or
a period. Examples of this latter case are the time
of shar’î zawâl, prayer times, and the time
wherein it becomes wâjib to perform
Qurbân.[1]
---------------------------------
[1] There is detailed information about Qurbân and how to
perform the Qurbân in the fourth chapter of the fifth fascicle of Endless
Bliss.
Clocks adjusted to local (mahallî) times in cities to the east are
ahead of those adjusted to the local times in the cities to the west on the
same day. The time of zuhr, that is, the canonical time of early afternoon
prayer begins a period of Tamkin later than true (astronomical) zawâl time at
every location. Since the adjustments of local clocks are different from one
another depending their longitudinal degrees, the prayer times on local clocks
on the same latitude do not vary with longitudinal variations. The adhânî time
clocks are local today, as they were formerly. Since the highest places of
different locations are not equal in height, the amount of Tamkin, and so the
canonical prayer times differ from one another by about 1 or 2 minutes, yet the
precautionary changes made in Tamkin eliminate such differences. In the present
time, clocks adjusted simultaneously to a wasâtî zawâlî (standard mean) time in
all cities of a country are used. In such a country where standard mean time is used, time for a certain
prayer in standard mean time is different even in the cities with the same
latitude. Four times the longitudinal difference between the two cities with
the same latitude shows the difference, in minutes, between the times for the
same prayer, in standard mean time, in those two cities. In short, only the
settings of local and standard time keeping clocks and the times of early
afternoon prayer (zuhr) do not change with latitude at places on the same
longitude. The advancement or retardation of a prayer time with increasing
latitude depends on its being in the forenoon or afternoon, or the season’s
being winter or summer, one being opposite of the other. The calculation of
prayer times from those for the latitude 41° N has been explained in the
instructions manual for the Rub’-i-dâira
(in Turkish). When longitudinal degrees change, i.e. at places with common
latitude, the adjustments of time clocks and all the prayer times on the common
time clocks change.
In all places between the two longitudes 7.5° east and west of London,
solar time for London (Greenwich Mean Time, GMT, or Universal Time, UT) is
used. This is called the West European Time. In places between seven and a half
degrees and twenty-two and a half degrees east of London, time one hour ahead
of it is used, which is called Central European Time. And in places between
22.5° and 37.5° of longitude east, time two hours ahead of GMT is used, which
is called East European Time. Times
three, four and five hours ahead of GMT are used
in the Near, Middle and Far East, respectively. Thus, there are twenty-four
zones of standard time on the globe, which follow one another by one hour. In a
country where such a standard time is
adopted, clocks are set to the local mean solar time of the places on the
standard meridian, which is one of the hourly
semicircles imagined to traverse that country with intervals of
fifteen degrees. The standard time of Türkiye is the local mean time of the
locations on the meridian 30° east of London, which is East European Time. The
cities Izmit, Kütahya, Bilecik and Elmalý lie on the meridian 30°. Some
countries do not use the time of the geographical zone they are in because of
political and economic reasons. For example, France and Spain use the Central
European Time. In the countries where different standard times are used, the
clocks in one show the time differently from those of another only in multiples
of hours at any given moment; the hourhand in an eastern country is in advance
of that in a western country.
The time for a prayer at a given place in Turkiye in local solar mean
time differs, in minutes, from Turkiye’s standard time by four times the
longitudinal difference between that place and the longitude 30°. To find the
time for this prayer in standard time, this difference will be subtracted from
or added to the local time if the longitudinal degree of that place is greater
or smaller than 30°, respectively. For example, let us say the time of a prayer
begins in the city of Kars at 7 hr 00 minutes in local mean time on May 1. The
city’s latitude is 41° and longitude is 43°, which is greater than 30°, local
time of Kars is ahead of the standard time. Then the time of that prayer begins
13 x 4 = 52 minutes earlier, at 6:08 in standard time.
The sum of Mg (the
time for midday (zawâl) in ghurûbî time) and St
(the time for true sunset in true solar time) for the same place is equal to 12
hours [equation (1), below], because this sum is a period of about 12 true
hours continuing from 12 o’clock in the morning in ghurûbî time to the time of
true sunset. Please see the chart for summer months. The unit of true solar
time is approximately equal to that of ghurûbî time.
Time of midday in
ghurûbî time+Time of sunset in true time=
=12hours or
Mg + St = 12 hours
(1)
And the sum of half of true daytime and half of true night-time Nt is about 12 hours. Therefore,
Half of true
nighttime+Time of sunset in true time=12hours or
(1 / 2) (Nt + St)=12 hours (2)
By combining the equations (1) and (2), we obtain:
Time of midday in ghurûbî time=Half of true nigthtime or
Mg = (1 / 2) Nt (3)
The time of (midday) in ghurûbî time is from the ghurûbî twelve in the
morning till the true midday. The ghurûbî twelve in the morning is half the
daytime later than midnight. It is before sunset in winter, and after sunset in
summer. The period for morning prayer, as well as that for fasting, begins at
the time of fajr-i-sâdiq. Its beginning is known when the adhânî clock, which
begins from 12 at the time of sunset, indicates the time of fajr, or when the
mean clock, which begins from 12 at the time of midninght, indicates the time
of fajr. Sunrise begins half the night-time later than 12 midnight, or a period
of night-time later than 12 at the time of sunset, or half the daytime earlier
than zawâl. Between the time of sunrise and (the ghurûbî)
If days and nights were equal in length, the Sun would always rise six
hours before and set six hours after the midday. Since they are not equal, the
period between the times of zawâl and ghurûb (sunset) is somewhat longer than
six hours in summer months. In winter months, on the other hand, this period
becomes a little shorter. This difference from six hours is called the nisf fadla = semi excess time. Likewise, In
summer months, true sunsets differ from the time of zawâl by the sum of six and
semi excess, whereas their difference in winter months is the difference of
semi excess from six. Conversely, the ghurûbî twelve in the morning is
transpositionally the same amount different from the time of zawâl.
To find the time of zuhr in adhânî time and the times of
sunrise and sunset in true and mean time, the nisf
fadla is obtained by British Mathematician John Napier’s formula. According to
this formula, on a spherical right triangle [for example, the triangle TCL in
Figure 2, page 142] cos of one of the five parts other than the right angle
[sin of its complement] is equal to the product of cot values of the two parts
adjacent to that part [tag of their complements], or to the product of the sin
values of the other two parts not adjacent to it. However, instead of the two
perpendicular sides themselves, their complements are included in the
calculation.
sin (nisf fadla)=tan (declination) x tan (latitude).
Using this formula and with the help of a scientific calculator or a
table of logarithms of trigonometric functions, the arc of nisf fadla in degrees and, multiplying this by 4,
its equivalent in minutes of true solar time is found. By adding the absolute
value of nisf fadla to 6 true solar hours (one-fourth of a true day) if the Sun
and the city are on the same hemisphere, (that is, if declination and latitude
bear the same sign), the time of calculated true sunset in local true solar
time is obtained. By subtracting the absolute value of nisf fadla from 6 hours,
the time of true midday (zawâl) in ghurûbî time, or the time of true sunrise in
true solar time, [beginning with midnight,] is found. In other words, the
ghurûbî
For instance, on May 1, the declination of the Sun is +14°55', the
Equation of Time is +3 minutes of time and Istanbul’s latitude is +41°;
depressing the keys,
14:55 ◦ﻭﻭﻭ→
tan x 41
tan = arc sin x 4 = ◦ﻭﻭﻭ→
on the scientific calculator (Privilege) gives the resultant 53min
33sec (of time). Nisf fadla is found to be 54min (of time); the calculated true
sunset is at 6:54 in true zawâlî time, at 6:51 in local mean zawâlî time, and
at 18:55 in standard time or at 19:55 in summer time. The time of canonical
sunset is found to be 20:05, in summer time, by adding the Tamkin of 10 minutes
for Istanbul.
Duration of true daytime is 13 hours plus 48
minutes, and duration of night is its difference from 24 hours, i.e. 10 hours
plus 12 minutes; 5:06, which is the difference between nisf fadla and 6 hours,
is the time of true sunrise in true time, i.e. from the time of midnight, or
the time of zawâl in ghurûbî time. The time of true midday in adhânî time is
earlier than that in ghurûbî time by a period of Tamkin, that is, at 4:56. The
canonical time of zuhr in adhânî time begins later than the time of true midday
in adhânî time by a period of Tamkin, that is, at 5:06. Twice the time of zuhr
in adhânî time, 10 hours and 12 minutes, is the approximate duration of
astronomical nighttime, and subtracting 20 minutes (twice the Tamkin) from this
gives 9:52 to be the time of canonical sunrise in adhânî time. If Equation of
Time and Tamkin are subtracted from 5 hours 6 minutes and the result is
converted to standard time, the time of canonical sunset is obtained to be
4:57. Subtraction of the time of adhânî zuhr from 6 hours yields the nisf fadla
time. Since the absolute declination of the Sun is 23°
Nisf fadla is zero, always at locations on the equator, and all over
the world on March 21st and on September 23rd, because the declination of the
Sun is zero always on the equator and on the whole world on March 21st and on
September 23rd. On April 1, declination of the Sun is 4°20' and the equation of
time is -4 minutes. The latitude of Vienna, Austria, is 48°15', and nisf fadla
is found, with the use of a scientific (Privilege) calculator by depressing the
keys, CE/C 4.20 ◦ﻭﻭﻭ→ tan x 48.15 ◦ﻭﻭﻭ→ tan = arc
sin x 4= ◦ﻭﻭﻭ→ to be about
19.5 minutes. Then, the time of the evening prayer [canonical sunset] in Vienna
begins at 6:33:30 in local mean solar time. Vienna’s longitude is 16°25', which
is 1°25' east of the (hourly) standard meridian; therefore, the time of evening
prayer begins at 6:27:50 in Austria’s geographical standard time, which is 1
hour ahead of GMT. Since the latitude of Paris is 48°50', nisf fadla is 20
minutes and the time of the evening prayer in local mean time begins at 6:34;
with its longitude +2°20' east, it should normally begin at 6:25 in the
geographical standard time, yet the standard time used in France
is 1 hour ahead of West European Time; so it
begins at 19:25. For New York, latitude is 41°, and nifs fadla is 15 minutes,
thus the time of evening prayer begins at 6:29 in local mean time; with
longitude -74°, it is 1° east of the (hourly) standard meridian -75° which
corresponds to the standard geographical time 5 [75 / 15] hours behind that of
London, and, in this time, the time of evening prayer begins at 6:25. For
Delhi, latitude is 28°45'; nisf fadla is 9.5 minutes, the time of evening
prayer begins at 6:23:30 in local mean time; its longitude is +77°, thus 2° east
of the standard meridian; it begins at 6:15:30 in standard mean time which is 5
hours ahead of London.
For Trabzon, latitude is the same (41°) as that for Istanbul, and
longitude is 39°50'. To find nisf fadla on May 1, the following keys of the
CASIO fx- scientific calculator are depressed:
ON 14 ◦ﻭﻭﻭ◦55 ◦ﻭﻭﻭ◦tan x 41 tan = INV sin x 4 = INV ◦ﻭﻭﻭ◦and the time of nisf fadla is found to be 53 minutes and 33 seconds, which is about 54 minutes.[1] Time of sunset, as in Istanbul, is at 7:01 in local mean time and at 6:22 in standard time, that is, 39 minutes before the former. Al-Makkat al-mukarrama is on latitude 21°26' and, like Trabzon, on longitude 39°50', and nisf fadla on May 1 is 24 minutes. Time of sunset is 6:31 in local mean time, and 5:52 in standard time, which is 39 minutes before this as adjusted for the standard meridian of longitude 30°. On November 1, declination is -14°16' and the equation of time is +16 minutes. Nisf fadla is 51 and 23 minutes for Istanbul and Mekka, respectively, while the time of sunset in standard time is 5:07 and 4:52 for Istanbul and Mekka, respectively. On November 1, evening adhân can be heard from a local radio broadcast in Mekka 15 minutes before the evening adhân in Istanbul. In the above calculations for sunset at various cities, the Tamkin for Istanbul is used. On the clocks set to adhânî and local mean times, the time of a prayer differs in cities with the same latitude by the amount of the difference between their tamkins only.
The time of zawâl in local mean solar time differs from 12 hours (in
local true solar time) by the Equation of Time, i.e. less than one minute,
everywhere, and ranges from up to 16 minutes before to 14 minutes past
---------------------------------
[1] The use or operation of calculators vary with brand.
longitudinal difference between the place in question
and the standard meridian of longitude 30° for every location in Turkey. And
the time of zawâl changes every day for an amount of up to one or two minutes
on the adhânî clocks. In the time of the Ottomans, there were muwaqqits (time-keepers) at great mosques who
were in charge of these adjustments.
To find the Equation of Time easily, the time for the early afternoon
prayer [zuhr] for Istanbul, for instance, on the day in question is taken from
a reliable calendar in standard time. This time minus 14 minutes is the time of
midday in local mean solar time. As the time of midday is 12 o’clock everywhere
in true solar time, the difference between these two midday times in minutes is
the equation of time. If the time of zawâl (midday) is earlier than 12:00 in
mean time, the sign of the equation of time is (+) and, if it is later, it is
(-).
Since the equation of time is -13 minutes on March
1, the time of zawâl in local mean solar time is at 12:13 everywhere. The time
for the early afternoon prayer is later than this by the amount of Tamkin. In
Istanbul, for example, it begins at 12:23. And at any place, its time in
standard time begins either earlier or later than its time in local mean time
by
an amount, in minutes, equal to four times the
longitudinal difference in degrees between the (hourly) standard meridian and
the meridian of the place in question. If a location in Turkiye is to the east
of the standard meridian 30° E, it is earlier, otherwise later. Thus, the time
for the early afternoon prayer in standard time is at about 12:11 in Ankara and
at 12:27 in Istanbul. When the clock, adjusted to standard time, arrives at the
time of early afternoon prayer, the adjustment of the clock keeping the adhânî
time is made for that day by setting it to the time of the early afternoon
prayer found using the nisf fadla. If the height of the highest place is
unknown, the period of Tamkin of a
location is found as: (1) the time between the moment when sunlight disappears
from the highest place and the instant when sunset is seen at the sensible
horizon, or (2) the difference between 12 and the time found by combining with
equation of time the time shown by the clock set to local mean time when it is
the time of zuhr found using nisf fadla on an adhânî clock set to 12 when the
sunlight is seen to disappear at the highest place of the location, or (3) the
difference between the time when sunlight disappears from the highest place in
local mean time and the time of sunset found by using nisf fadla; or (4) the
period of time determined by adding the equation of time if it is (+) positive
to (and, if it is negative, subtracting from) the difference of time of zuhr in
local mean time and 12:00.
It is written as follows in Radd al-muhtâr by Ibn Âbidîn, as well as in
the Shâfi’î book Al-anwâr and in the
commentary to the Mâlikî book Al-muqaddamat
al-izziyya, an in al-Mîzân ul-kubrâ
“For a salât (prayer) to be sahîh (valid), one should perform it after its time
has begun and know that one is performing it in its correct time. A salât
performed with doubtful knowledge as to the arrival of its correct time is not
valid (sahîh) even if you realize, after perming it, that you performed it in
its correct time. To know that the prayer time has come means to hear the adhân
recited by a just (’âdil)[1] Muslim who knows the prayer times. If the reciter
of the
---------------------------------
[1] A Muslim who never commits a grave sin and who does not commit venial sins continually and whose good deeds are more than his wrongdoings, is called an 'âdil Muslim. On the other hand, 'fâsiq means a Muslim who is habituated to committing one of the grave sins such as fornication, gambling, consumption of hard drinks, usury (however low the rate of interest), looking at people or things or
adhân is not just [or if there is not a calendar
prepared by a just Muslim], you investigate whether the time has come and he
should perform it when you surely believe that it is the time. Information
obtained from a sinner (fâsiq). or a person who is not known to be a just
(’âdil) Muslim concerning the direction of qibla or other religious matters
such as cleannes or uncleanness of something, or whether a certain act (or
behaviour or thought) is halâl (permitted) or harâm (forbiddin), as well as his
reciting the adhân, is not dependable; instead of asking a person of that kind,
you have to learn the matter in your own and act in accordance with the result
of your personal research.”
It is mustahab to perform the morning prayer when it gets rather light
everywhere in every season; this is called “isfâr”.
It is mustahab to perform the early afternoon prayer in jamâ’a late on hot days
in summer and early on winter days. Performing the evening prayer early is
mustahab always. And it is mustahab to perform the night prayer as late as
one-third of the canonical night, i.e., by the end of the first one-third of
the time between ghurûb (sunset) and fajr (dawn). It is makrûh tahrîmî to
postpone it beyond the time of midnight. These postponements apply only to
those who perform namâz in jamâ’a. One who performs alone at home should
perform every prayer as soon as its time begins. A hadîth
sherîf reported in Kunûz ad-daqâ’iq
on the authority of Hâkim and Tirmidhî says: “The
most valuable ’ibâda is the salât performed in its early time.”
Another hadîth sherîf, reported in the Sahîh of Muslim and also written on page 537 of Izâlat al-khafâ[1], declares: “Such a time will come when
directors and imâms will kill the salât; [that is,] will postpone it to later than
its [prescribed] time. You should perform your
salât in its time! If they perform in jamâ’a
---------------------------------
.images that are forbidden for a Muslim to look at, condoning acts of wrongdoing committed by a person under his responsibility such as his wife or daughters, for instance their going out without covering those parts of their body which Islam commands them to cover. Also, a Muslim who habitually neglects one of Islam's open commandments such as the daily five prayers of namaz, etc, as well as one who ignores learning something which is farz or wâjib for a Muslim to learn, is 'fâsiq'. Hence, 'âdil and fâsiq are antonymous.
[1] Izâlat-ul-khafâ an
khilâfat-il-khulafâ, by
the great Sunnî Islamic scholar
Shâh Waliyyullah Dahlawî (1114 [1702 A.D.]-1176 [1762]; Delhi).
after you [have performed], perform it again together with
them! The one you perform the second time will become nâfila (supererogatory).” It will be precautionary to
perform the late afternoon and night prayers according to Al-Imâm al-a’zam’s
report. He who will not be able to wake up later should perform the witr prayer
right after the night prayer. He who performs it before night prayer should
reperform it. And he who can wake up should perform it towards the end of the
night.
Ahmad Ziyâ Bey provides the following information on page 157: In a
city, the algebraic sum of a prayer’s canonical time known with respect to the
local mean time and the equation of time for the day in question is its time
with respect to the true solar time. This plus the time of zuhr in adhânî time
and minus one unit of Tamkin yields the prayer’s canonical time with respect to
the adhânî time. If the result exceeds twelve, the excess indicates the adhânî
time. For example, the Sun sets at 18:00 (6:00 p.m.) in standard time in
Istanbul on March 1. Since the equation of time at the time of sunset is -12
minutes, the time of canonical sunset in Istanbul is 5:44 in local true solar
time. And since the time of canonical zuhr in adhânî time is 06:26, the time of
sunset is 06:26+05:44-10 minutes=12:00. In general,
(1) t in adhânî time = t at the same moment in true solar
time + t of zuhr in adhânî time - Tamkin of the location
(2) t in true solar
time = t in adhânî time + t of canonical sunset in true solar time
where t is time.
In the equation (2), if the time
of sunset is in mean time, the zawâlî time obtained is also mean.
The equation (2) may also be
written as:
(3) t in adhânî time =
t in true solar time - t of canonical sunset in true solar time
If the time of sunset treated is greater than the true time, the
subtraction must be done after twelve is added to the true time.
The zawâlî time in the equations (2)
and (3) is given in true solar time,
yet, since the same numbers are added and then subtracted while converting
standard time to true time and then the true time found to standard time, the
computation done without converting standard time to true time yields the same
results, that is:
(4) t in standard time
= t in adhânî time + t of canonical sunset in standard time
(5) t in adhânî time = t in standard time - t of canonical
sunset in standard time
The time of sunset on March 1 as calculated above can also be found out
with the help of the last equation: 18:00 - 18:00 = 00:00, which is 12:00 in
adhânî time. Likewise, since the time for the late afternoon prayer is 15:34
and the time of sunset is 6:00 in standard time on March 1, the time for the
late afternoon prayer in adhânî time is:
15:34 - 6:00 = 9:34.
Similarly, since the time of imsâk in adhânî time on the same day is
10:52, the time of imsâk in standard time is 10:52+6:00=16:52 or 4:52 p.m. by
the equation (4).
Let us find the time of sunset in true solar time in Istanbul on 23
June 1982 Wednesday, 1 Ramadan 1402: on that day, the time for the early
afternoon prayer in Istanbul is 4:32 in adhânî time, and the Equation of Time
is -2 minutes. The time of sunset in local true solar time in Istanbul is the
difference between this and 12 hours, that is, 7:28. The canonical sunset is at
7:38 in true solar time, at 19:40 in mean solar time, at 19:44 in standard time
of Türkiye and at 20:44 in summer time.
If the time in standard time is smaller than the time of sunset, 12 or
24 is added to it in the equations (3)
and (5). Ahmad Ziyâ Bey employs the
formulas
(6) t in adhânî time = true time of zawâl + true solar time
and
(7)true solar time = adhânî time-true time of zawâl.
Mustafa Efendi, Head of Astronomers in the Ottoman Empire, wrote in the
pocket calendar of
To determine the time the Sun comes to the altitude for the beginning
of the time of a certain salât, first the value of fadl-i
dâir (time corresponding to the hour angle of the Sun) is
calculated. Fadl-i dâir is the interval between the point where the center of
the Sun is and the time of zawâl (midday) for the daytime, and it is the
interval between that point and midnight for the nighttime. The angle of fadl-i
dâir, H, can be calculated from the formula for the spherical triangle: [See
figure: 1]
H sin(M-.90° + δ) x
sin(M-.90° + φ)
Sin ----= √------------------------------------------------ (1)
2
sin(90° - δ) x sin(90°
- φ)
where d is the declination of the Sun and ö is the latitude of the
location and M is the half of the sum of the three sides of the spherical
triangle and determined with the formula:
(90° - δ) + (90°
- φ) + (90°
- h)
M = ------------------------------------------------
2
where h is the altitude of the Sun. The sign of altitude is (+) above
the true horizon and (-) below it. If declination and altitude have opposite
signs, the declination added to 90°, instead of its complementary to 90°, is
taken.
The
formula for fadl-i dâir is simplified by substituting the value of M as
Z + ∆ Z - ∆
sin ----------- × sin ---------
H 2 2
sin ---- = √----------------------------------------------- (2)
2 cos φ
× cos δ
Here, the interval represented by the angle H is
measured in reference to the meridian (nisf an-nahâr), and:
∆ =
90° - GI = (latitude of location) -
(declination of the Sun) = φ - δ,
where GI is the angle ghâyat irtifa’ = maximum altitude of the Sun’s centre
(at midday).
Z (angular distance to the zenith) = 90° - (azimuthal zenith), which
represents the angle of Fay-i zawâl
formed by the two straight lines which start from the top of the pillar, one
extending in the direction of meridian and the other in the direction of the
surface of the earth.
The variables are substituted into the formula with their algebraic
signs.
Let us calculate the time of ’asr awwal, that is, the early time of the
late afternoon prayer in Istanbul on August 13. Assuming that a stick of
tan Z1 = tan (90° -h1) = 1 + fay-i
zawâl = SAA
where Z1 is the angle complementary to the altitude h1 for ’asr awwal,
SAA is the [the length of stick’s] shadow at ’asr awwal, and
fay-i zawâl = tan CGI = tan ∆
where CGI is the angle complementary to ghâyat irtifâ’ (altitude of the
centre of the Sun at midday). Ghâyat irtifâ’, GI =
maximum altitude of the Sun at the time of zawâl is determined by
adding the declination to the angle complementary to latitude if the signs of
both are the same, that is, when both of them are on the same hemisphere, or by
subtracting the declination from it if they have opposite signs, that is, when
they are on different hemispheres. If the sum of the angle complementary to
latitude and declination is more than 90°, its difference from 90° is the GI,
and the Sun is in the eastern side of the sky. If latitude and declination are
on the same side, their difference or, if they are on different sides, their
sum gives the complementary to GI (∆).
GI = 49°00' + 14°50' =
63°50'
log (fay-i zawâl) = log tan 26°10' = `1.69138
Fay-i zawâl =
tan Z1 = tan (90° -h1) = 1.4913 and using the table of logarithms of
trigonometric functions,
log tan Z1 = 0.17357
or with a Privilege calculator, the operations:
1. 4913 arc tan ◦ﻭﻭﻭ→ give:
90° - h = azimuthal distance = Z1
= 56°09'
75° 10’
+ 49° + 56° 09’
M = ----------------------------------------------
= 90° 10’
2
Sin ----= √-------------------------------
2 sin 75° 10’ . sin
49°
and using the table of logarithms of trigonometric
functions,
H 1
Log sin ----= ---- [(1.41300 + 1.81839) – (1.98528 + 1.87778)]
2 2
1 1
= ----- (1.23139 - 1.86306) = ------ (1.36833) = 1.68417
2 2
(1/2) H=28°54' and H=57°48' and multiplying this by 4 we get 231.2
minutes of time, that is, 3 hours 51 minutes, which is the period of fadl-i
dâir (hour angle) for the ’asr awwal on August 13th in Istanbul. Since the true
time is 00:00 at the time of true zawâl, it is directly the time of true ’asr
awwal in true time and is three hours and fifty-one minutes, which is equal to
the time for the rod’s shadow to lengthen by a length equal to its height after
the time of true zuhr. Canonical time of ’asr awwal in reference to canonical
zuhr is later than this by the amount of the Tamkin of that location. Since the
Equation of Time is -5 minutes, it is 16:10 in standard time. If the time of
sunset in standard time, 7:12, is subtracted from this standard time, time for
the late afternoon prayer in Istanbul is obtained in adhânî time to be 8:58,
using equation (5) on page 155. When the (time termed) fadl-i-dâir is added to
the adhânî time of zuhr, i.e. the true time of zawâl with respect to the
ghurûbî time, which is five hours and seven minutes, the result is both the
true time of late afternoon prayer in ghurûbî time and the canonical time of
’asr-i-awwal in adhânî time. For, although the canonical time of ’asr-i-awwal
is one unit of Tamkin later than this sum, i.e., than the ghurûbî true time,
its canonical time in adhânî time is one unit of Tamkin earlier than that
ghurûbî shar’î time. Similarly, the canonical times of early afternoon, evening
and night prayers in adhânî time are the same as their true times found by
calculation in ghurûbî time.
Another method applicable for determining the altitude for the
’asr-i-awwal (the early time for late afternoon prayer) is as follows: the time
when the Sun reaches maximum altitude is determined graphically by measuring or
calculating, and using the relation
Length of shadow = cot h,
the length of the shadow of a
The ’asr thânî time of early afternoon prayer (, i.e. the later time
for late afternoon prayer,) can be found by utilizing the same formula, yet in
this case:
tan Z2 = 2 + fay-i zawâl = SAT
where Z2 is the angle
complementary to the sun’s altitude for ’asr thânî = azimuthal distance, and SAT is the [length of the stick’s] shadow at ’asr
thânî.
Z2 = 68°
M = 96°09' and
H= 73°
The time of fadl-i dâir is 4 hours 55 minutes. When the Tamkin is added
to this, the ’asr thânî comes out to be 5:05 for Istanbul in true solar time.
To determine the time of the ’asr-i-awwal for late afternoon prayer,
first the angle Z, complementary to altitude h, and then fadl-i dâir are
calculated using the formula:
Z1 = azimuthal distance = arc tan (1 + tan ∆),
and for the ’asr-i-awwal:
Z2 = arc tan (2 + tan ∆),
where tan ∆ is fay-i
zawâl. The angle whose tangent is equal to the sum of tan ∆ with 1 or 2
is the value of Z (complementary to the altitude) for late afternoon prayer.
At the ’ishâ awwal of night prayer, the center of the Sun is 17° below
the true horizon; in other words, its true altitude is -17°. Since the
declination plus 90° is taken into account instead of the angle complementary
to the declination:
104° 50’ + 49° + 73°
M = --------------------------
= 113° 25’ and H = 50° 53’
2
and the time of fadl-i dâir = hour angle is 3 hours 24 minutes,
which is the interval from the time for night
prayer in true time to midnight. 10 minutes of Tamkin at the time of ’ishâ for
Istanbul is added to the difference between that time [of fadl-i dâir] and 12
hours, since the center of the Sun leaves the canonical horizon later and
naturally its rear edge leaves the horizons even later. On August 13, the time
for the night prayer is 8:46 in true solar time and 20:55 in standard time. By
subtracting the time of fadl-i dâir from the time for the noon prayer, 5:07,
which is half of the astronomical night time, the time of canonical ’ishâ awwal
and astronomical time with regard to the ghurûbî time is found to be 1:42 in
adhânî time, without taking into account here the Tamkin at the time of ’ishâ
which would be subtracted and then added.
104° 50’
+ 49° + 71°
M = --------------------------------
= 112° 25’ and H = 47° 26’
2
On August 13, the center of the Sun is the sum of 19° and altitudinal
angle below the true horizon, when the whiteness called fajr-i sâdiq begins to
dawn; in other words, its true altitude differs from -19°. Hence:
and dividing this by 15, we get the time of fadl-i dâir (hour angle) to
be 3 hours 10 minutes, which is the interval between the Sun’s center and
midnight. This is the time of imsâk in true time since the true time is 00:00
at midnight. The Tamkin, 10 minutes, is subtracted from this, because the Sun’s
altitude of -19° is closer to the canonical horizon than it is to the true
horizon and naturally the upper edge of the Sun is closer to the horizons than
its center. Then, the time of imsâk is 3:00 in true solar time of Istanbul and
3:09 in standard time. If fadl-i dâir is added to the time of zuhr, i.e.
(5:07), which is equal to half of the night-time, and then 20 minutes of Tamkin
is subtracted, the time of imsâk comes out to be 7:57 in adhânî time. The
fadl-i dâir found on the programmable CASIO fx-3600p calculator is 8 hours 50
minutes, which is the interval from the fajr (dawn) to the zawâl (midday). To
find its difference from midnight, this is subtracted from 12 hours, which
yields fadl-i dâir to be 3 hours 10 minutes, again. See instructions booklet
for Rub’-i-dâira.
The period between dawn and sunrise is called hissa-i fajr = duration of dawn, that between
dusk and sunset is called hissa-i shafaq = duration
of dusk. If the fadl-i dâir of dawn or dusk is subtracted from the
adhânî zuhr time, [i.e., from midnight,] or if
nisf fadla is added (for winter) to or subtracted
(for summer) from the complementary to the fadl-i dâir of dawn or dusk, these
hissas = durations are obtained. Since the signs of the altitudes for fajr and
shafaq are (-), their fadl-i dâirs begin from midnight.
Ahmad Ziyâ Bey wrote: “The ’ulamâ’ of Islam reported the time of imsâk
to be the time of the first sighting of whiteness on the horizon, not the time
when it spreads along it.” Some European books, however, define the time of
dawn as the time when the spread of redness, which begins later than whiteness,
along the horizon is completed, thus taking into account the true altitude of
the Sun 16° below the horizon. As it has been observed since 1983, some people
who publish calendars act under the guidance of those European books and base
their calculations of the time of imsâk on 16° below the horizon. Those who
begin fasting according to such calendars continue eating sahûr meal till 15 to
20 minutes after the times prescribed by the Islamic scholars. Their fast is
not sahîh. On the first and last pages of the pocket calendar Takwîm-i Ziyâ for 1926 (Hijrî lunar 1344, solar
1305) by Ahmad Ziyâ Bey, it is stated: “This calendar has been printed after
the examination carried out by the Board of Consultation and a certification
granted under the authority of the Great Head Office of the Religious Affairs.”
The prayer times approved by a Board composed of an astronomer and eminent
Islamic scholars should not be altered. Some details on this topic have been
given by Elmalýlý Hamdi Yazýr in the twenty-second volume of the magazine Sabîl-ur-reshâd.
Because the declination of the Sun changes every moment, its hourly
declination should be used in order to obtain accurate results.
For example, let us examine the accuracy of our clock in the afternoon
on May
16°06' on May 5. The difference in declination is
There is another formula, more suitable to scientific calculators, for
finding the angle of fadl-i dâir, the hour angle, H :
Sin h ±.(sin
δ x sin φ)
Cos H = -----------------------------
(3)
(cos δ x cos φ)
where h is the altitude, δ is
declination and φ is latitude. Hence
Sin 49° 10’ –[sin (15° 58’)
x sin (41°)]
Cos H = -----------------------------------------------
(cos 15° 58’ x cos 41° )
0.7566
– (0.2750 x 0.6561) 0.7566 –
0.1805
= ----------------------------------
=--------------------
0.9614 x 0.7547 0.7256
0.5762
= ----------- =
0.7940
0.7256
This gives H=37°26' and, dividing this by 15, we get fadl-i dâir to be
2 hours 30 minutes, which is in true solar time. To obtain this result, the
following keys of a Privilege calculator are depressed:
CE/C 15.58 ◦ﻭﻭﻭ→ cos x 41 cos = MS 49.10 ◦ﻭﻭﻭ→ sin -
15.58 ◦ﻭﻭﻭ→ sin x 41
sin = ÷ MR = arc cos x 4 = 149.7 minutes of time, which is the result read on
the screen.
Since the equation of time is +3 minutes on May 4, it is 2:31 in
standard time; hence we see that our clock is approximately 7 minutes fast.
In the equation (3) for cos H, the absolute values of the variables
were substituted. If the city and the position of the Sun are on the same
hemisphere, i.e., if the latitude of the city and the declination of the Sun
have the
same sign, the (-) sign in the numerator of the
formula is used when the Sun is above the horizon, i.e., during the day time,
while the (+) sign is used during the night. If vice versa, the opposite is
done. Fadl-i dâir (hour angle) calculated in this way is the interval between
the point where the center of the Sun is and the time of midday (nisf an-nahâr)
during the day, or between that point and midnight during the night. The same
formula may also be used with only the minus sign in the numerator. In that
case, all figures will be substituted with their signs and the resultant H will
always be measured from the meridian (nisf an-nahâr).
Let us find the fadl-i dâir according to the second form of the formula
(3): on the Privilege calculator, depressing the keys
49.10 ◦ﻭﻭﻭ→ sin - 15.58 ◦ﻭﻭﻭ→ MS sin x 41
sin = ÷ MR cos ÷ 41
gives 2hr 29 min 44.59 sec showing fadl-i dâir to be about 2 hours 30
minutes.
To correct the apparent altitude of the upper edge of the Sun with
respect to the mathematical horizon measured by using an astrolab, the
corresponding refraction of the atmosphere and the apparent radius of the Sun
are subtracted from and the parallax is added to this altitude, and thus the
true altitude of the center of the Sun with respect to the true horizon is
obtained. In the book Rub-i-dâ’ira by
Ahmad Ziyâ Bey, it is written that the calculation of the times of ishrâq and
isfirâr, as well as checking the accuracy of our clock, (explained a few pages
earlier,) is possible.
We shall now find the time for salât al-’îyd[1], that is, the time of ishrâq, in Istanbul on
January 11. This is the time when the lower edge of the Sun is as high as the
length of a spear from the line of the apparent horizon, which corresponds to a
5° altitude of its center from the true horizon. The declination of the Sun is
-21°53', and it is -21°44' on the next day. The daily difference of declination
is
ON 5 sin - 21 ◦ﻭﻭﻭ◦
51
◦ﻭﻭﻭ ± sin x 41 sin = ÷ 21 ◦ﻭﻭﻭ◦
51
◦ﻭﻭﻭ
---------------------------------
[1] Salat al-'iyd, or namâz of 'iyd, is dealt with in detail in
chapter 22.
± cos ÷ 41 cos = INV cos ÷ 15 = INV ◦ﻭﻭﻭ
the calculator (CASIO fx-3600 P) reads 4:07. The difference between the
fadl-i dâir and midday [12:00], 7:53, is the time of ishrâq with respect to the
centre of the Sun in true time. Since the equation of time is -8 minutes, it is
8:05 in standard time. 10 minutes of precaution is added and 8:15 is written in
calendars. If fadl-i dâir is subtracted from the adhânî time of zuhr [7:22],
the time of ishrâq is found to be 3:15 in ghurûbî time. As a precaution, the
time of salât al-’îd has been taken forward as much as the amount of Tamkin,
and, for this purpose, the time of ishrâq in adhânî time has been written in
calendars without subtracting the Tamkin. Kadûsî
says at the end, “Two units of tamkin [5°] is, in winter subtracted from and,
in summer, added to twice the amount of nisf fadla and the angle complementary
to the sum is converted to hours and added to 6. The result is the time of
sunrise in adhânî time. If two tamkins are added instead of subtracting and
subtracted instead of adding and as a precaution a Tamkin is added to the
result, the time of ishrâq is obtained.”
The treatise by Kadûsî, the booklet Irtifâ’,
was written in
On the same day, the time of isfirâr-i
shams is the time when the front [lower] edge of the Sun approaches
the line of the apparent horizon as much as the length of a spear, that is, the
time when the center of the Sun is at an altitude of 5° from the true horizon.
Since isfirâr is approximately 16 hours later than midnight, and since the
difference between the times of Istanbul and London is 1 hour and 56 minutes,
declination at that time is 5'16.5" less than that at midnight, that is,
it is -21°47' 43.5". Depressing the following keys of the programmable[1] CASIO fx-3600 P
calculator:
P1 5 RUN 21 ◦ﻭﻭﻭ◦
47 ◦ﻭﻭﻭ◦ 43.5 ◦ﻭﻭﻭ ± RUN 41 RUN
fadl-i dâir is easily found to be 4 hours 7 minutes 20.87 seconds.
Since the true time is 00:00 at zuhr, the time of isfirâr is represented only
by fadl-i dâir to be 4:07 in true time, while it is 4:15 in mean solar
---------------------------------
[1] To make the related
programme, for example on the CASIO calculator,
this succession is followed:
MODE ![]() P1 ENT sin —
Kin 1 sin x ENT Kin 3 sin = ÷ Kout 1
cos ÷ -Kout 3 cos = INV cos ÷ 15 =
INV ◦ﻭﻭﻭ MODE
P1 ENT sin —
Kin 1 sin x ENT Kin 3 sin = ÷ Kout 1
cos ÷ -Kout 3 cos = INV cos ÷ 15 =
INV ◦ﻭﻭﻭ MODE
![]()
time and 4:19 in standard time. From the sum of
the time of zuhr in adhânî time and fadl-i dâir, 11 hours 29 minutes, which is
the time of isfirâr in ghurûbî time, a Tamkin is subtracted and the remainder,
11:19, is the time of isfirâr in adhânî time. The time of isfirâr-i shams can
also be obtained by subtracting an amount of time one unit of Tamkin shorter
than the time of ishrâq written in calendars from the sum of the time of sunset
and the time of sunrise in adhânî or local or standard the difference of time
between the times of isfirâr and sunset is ten minutes shorter than that between
the times of ishrâq and sunrise.
The following keys are depressed in order to adjust the CASIO fx - 3600
P calculator so as to use it in the calculation defined above: MODE P1 ENT sin
- ENT Kin 1 sin x ENT Kin 3 sin = ÷ Koul 1 cos ÷ Kout 3 cos = INV cos ÷ 15 =
INV ◦ﻭﻭﻭ MODE ![]()
Let us find the times (’asr awwal and thânî) of the late afternoon prayer in Istanbul for February the 1st. The declination of the Sun is -17°15' (at time 00:00:00 and -16°58' at 24:00:00) and the equation of time is -13 min 31 sec (at time 00:00:00 and -13 min 39 sec at 24:00:00) (for the solar years 1990+4n). Since Fay-i-zawâl = tan (complement of maximum altitude, which inturn is: φ - δ , first, the altitudes are found utilizing the formulas:
tan Z1 = 1 + tan (φ - δ)![]() and
and
tan Z2 = 2 + tan (φ - δ)
where φ is latitude δ is
declination, Z1 is the angle complementary to the altitude for ’asr awwal and
Z2 is the angle complementary to the altitude for ’asr thânî. The operations,
CE/C 41 - 17.15 ◦ﻭﻭﻭ→ ± = tan + 1 = arc tan MS 90 - MR = ◦ﻭﻭﻭ→
gives the altitude for ’asr awwal to be 20°55' while the operations,
20.55 ◦ﻭﻭﻭ→ sin - 17.15 ◦ﻭﻭﻭ→ - ± MS sin x 41
sin = ÷ MR cos ÷
41 cos = arc cos ÷ 15 = ◦ﻭﻭﻭ→
gives fadl-i dâir to be 2 hours 40 minutes on a Privilege calculator.
Adding Tamkin of 10 minutes for Istanbul to the latter, the time for ’asr awwal
comes out to be 2:50 in true solar, 13:04 in mean solar and 3:08 in standard
time. Addition of fadl-i dâir to the adhânî time of zuhr (7:03) gives ’asr
awwal to be 9:43 in ghurûbî and in adhânî times.
CE/C 41 - 17.15 ◦ﻭﻭﻭ→ ± = tan + 2 = arc tan MS 90 - MR = ◦ﻭﻭﻭ→
gives the altitude for ’asr thânî to be 15°28' while the operations,
15.28 ◦ﻭﻭﻭ→ sin - 17.15 ◦ﻭﻭﻭ→ ± MS sin æ 41
sin = ÷ MR cos ÷
41 cos = arc cos ÷ 15 = ◦ﻭﻭﻭ→
gives fadl-i dâir to be 3 hours 21 minutes. The time for ’asr thânî
comes out to be 3:31 in true solar, 15:45 in mean solar, 15:49 in standard and
10:24 in ghurûbî and in adhânî times.
We may find the time of imsâk on August 13 also with the use of the
first form of the eqution (3)
CE/C 19 sin + 14.50 ◦ﻭﻭﻭ→ MS sin æ 41
sin = ÷ MR cos ÷ 41
cos = arc cos ÷ 15 = ◦ﻭﻭﻭ→
gives fadl-i dâir (time of hour angle) to be 3 hours 10 minutes. The
time of imsâk for Istanbul in true solar time is obtained to be at 3:00 hours
in true solar time by subtracting 10 minutes of Tamkin and adding it to
midnight.
Subtracting the fadl-i dâir calculated for fajr-i sâdiq from 12 hours
(00:00:00 or 24:00:00 hours) and adding 10 minutes of Tamkin, we obtain the
time of ’ishâ thânî for the night prayer to be exactly 9 o’clock in true solar
time. Adding the fadl-i dâir to the adhânî time of zuhr corresponding to midnight,
[05:07], and subtracting 20 minutes (two Tamkins), we obtain 7:57, which is the
adhânî time of imsâk.
Let us defermine the time of ’ishâ’-i-awwal on August 13 (in a 1990+4n
solar year). On a programmed CASIO fx-3600 P, keying.
P1 17 + ± RUN 14 ◦ﻭﻭﻭ◦
50 ◦ﻭﻭﻭ◦ RUN 41 RUN
the fadl-i dâir, FD=H is found to be 08:36 hours. Since true time is
00:00 hours at the time of zawâl, the time of ’ishâ-i-awwal, by adding 10
minutes of Tamkin, is found to be 8:46 pm (or 20:46) in true time, 8:55 (or
20:55) in standard time. As the time of zuhr in adhânî time is 5:07, the adhânî
time of ’ishâ’-i-awwal is 13:41 hours or 1:43 pm.
Time for late afternoon prayer found, using the equation with the
square root, for August 13 can also be calculated using the electronic
calculator (light-operated CASIO), depressing the keys:
gives 0.4913 as fay-i-zawâl; depressing the keys,
ON 1.4913 INV tan INV ◦ﻭﻭﻭ
gives 56°09' as the angle complementary to the altitude for ’asr awwal,
and depressing the keys,
75 ◦ﻭﻭﻭ◦ 10 ◦ﻭﻭﻭ◦ + 49 + 56 ◦ﻭﻭﻭ◦ 9 ◦ﻭﻭﻭ◦ = ÷ 2 = INV ◦ﻭﻭﻭ
gives M to be 90°09'30", and depressing the keys,
ON 15 sin x 41 ◦ﻭﻭﻭ◦ 10 ◦ﻭﻭﻭ◦ sin ÷ 75 ◦ﻭﻭﻭ◦ 10 ◦ﻭﻭﻭ◦ sin ÷ 49 sin = √INV sin x 2 ÷ 15 = INV ◦ﻭﻭﻭ
fadl-i-dâir is calculated as 3 hours 51 minutes.
Since the altitude for ’asr-i awwal is 33°51', using a battery operated
programmable CASIO calculator, if we depress on the keys
P1
33 ◦ﻭﻭﻭ◦
51 ◦ﻭﻭﻭ◦
RUN 14 ◦ﻭﻭﻭ◦
50 ◦ﻭﻭﻭ◦ RUN 41 RUN
the time of hour angle, H is found to be 3 hours 51 minutes.
THERE ARE THREE TIMES WHEN IT
IS MAKRÛH TAHRÎMÎ, THAT IS, HARÂM, TO PERFORM SALÂT. A salât is not sahîh (valid) if it is fard and
is started at one of these times. If it is supererogatory, it will be sahîh but
makrûh tahrîmî. Supererogatory prayers begun at these times must be stopped and
performed later (qadâ). These three times are the period of sunrise, that of
sunset and the period when the Sun is at zawâl, i.e. at midday. In this sense,
the period of sunrise begins when the upper edge of the Sun is seen on the
horizon and ends when it shines too brightly to be looked at, i.e., at the time
of ishrâq; the period of sunset in a
dustfree, smogless, clear sky begins when the Sun or the places where its light
emanates become yellow enough to be looked at, and ends as it sinks (at the
horizon). This time is termed isfirâr-i-shams.
In calculations, the time of ishrâq has been taken forward by the addition of
Tamkin as a precaution, but the time of isfirâr has not been changed. “To
perform salât at midday” means that the first or
the last rak’a of it is performed at midday. This fact is written in Ibn
’Âbidîn, and in the annotation of Marâqil-falâh,
by Tahtâwî.
As stated above, not the various apparent altitudes relative to the
lines of different visible horizons of different heights but the canonical
altitudes relative to the location’s established canonical horizon should be
taken into account in calculations of all prayer times. Accordingly, the time
of canonical zawâl is the period between the two times when the front and rear
edges of the Sun are at their daily ultimate altitudes from the canonical
horizons at the places of rising and setting. It is equal to twice the amount
of Tamkin for that city. For example, at the time of true zawâl in Istanbul on
May 1, the ghâyat irtifâ’ = maximum altitude of the center of the Sun from the
true horizon is 49°+14.92°=63.92°. This is the same altitude from the true
horizon at which it sets and rises. The interval of fadl-i dâir is H=00:00:00
for this altitude. True zawâl in true time is always at 12:00 everywhere.
However, the time of canonical zawâl corresponding to its daily ultimate
altitude from the canonical horizon in the eastern side begins one period of
Tamkin earlier than 12:00. And the time of canonical zawâl corresponding to its
daily ultimate altitude relative to the canonical horizon in the western side
comes later than the true zawâl by the amount of Tamkin. In other words, the
time of canonical zawâl for Istanbul begins 10 minutes earlier than 12:00 in
true time. In standard time, the canonical zawâl period begins at 11:51 and
ends at 12:11 because the Equation of Time is +3 minutes. The time of zuhr, as given in calendars, for
those who are unable to see the Sun starts at this time. The interval of 20
minutes between the two is the time of zawâl, or makrûh
time, for Istanbul. [See page 127 and the translation of Shamâil-i Sherîfa, by Husamaddîn Efendi.].
Since the true altitude, h, of the Sun is zero at the times of true
sunset and sunrise, the Equation 3 on page 159 becomes - tan d x tan ö = cos H.
Hence, on May 1, cos H=-0.23, the angle of fadl-i-dâir = 103.39° and H=6:54,
and the time of true sunset is at 6:54 in true time, at 6:51 in local mean
time, and at 6:55 in standard time; and the time of sunrise in true
time=12:00-H=5:06, which corresponds to 5:03 in mean time. To find the time of
canonical sunrise, the Tamkin at sunrise for Istanbul, i.e. 10 minutes, is
subtracted from this. 4:53 is the remainder, which corresponds to 4:57 in
standard time.
The time of zuhr in adhânî time is 5:06, from
which [or from its sum with 12:00] fadl-i dâir is subtracted to yield the time
of true sunrise in ghurûbî time, and subtracting twice the Tamkin from this,
the time of canonical sunrise is obtained to be 9:52 in adhânî time. The time
of true sunset in ghurûbî time and that of canonical sunset in adhânî time are
12:00 hours, which is, at the same time, the sum of the time of zawâl in
ghurûbî time and the time of fadl-i-dâir, i.e. 5.06+6.54=12 hours.
The velocity of light is
While the Sun is setting, only the late afternoon prayer of that day
may be performed. According to Imâm Abû Yûsuf, it is not makrûh only on Friday
to perform supererogatory prayer when the Sun is at its maximum altitude, which
is a weak report (qawl da’îf). At any of these three times, (, i.e. the period
of sunrise, that of sunset, and the period when the Sun is at zawâl,) the salât
for a janâza[1] that was prepared earlier (than the
---------------------------------
[1] There is detailed
information about death, preparation for death, and salât of janâza in the thirteenth chapter of the fifth
fascicle of Endless Bliss.
beginning of the makrûh period) or sajda-i tilâwat
or sajda-i sahw are not permissible, either. But it is permissible to perform
the salât of a janâza if the preparation for burial is finished within (one of)
those [makrûh] times.
There are two periods of time in which it is makrûh to perform only
supererogatory salât. From dawn till sunrise in the morning no supererogatory
other than the sunna of morning prayer should be performed. After performing
the late afternoon prayer, it is makrûh to perform any supererogatory prayer
within the period between that time and evening prayer. It is makrûh to begin
performing the supererogatory, that is, the sunna, when the imâm mounts the
minbar on Friday and as the muezzin (or muadhdhin) says the iqâma and while the
imâm leads the jamâ’a at any other prayer time; an exception from this is the
sunna of morning prayer, which must be performed far behind the lines of jamâ’a
or behind a pillar. There are some scholars who say that the sunna which has
been started before the imâm mounted the minbar must be completed.
If the Sun begins to rise as you are performing morning prayer, the
prayer will not be sahîh. If the Sun sets as you are performing late afternoon
prayer, the prayer will be sahîh. If a person flies towards west by plane after
performing evening prayer and if he sees the Sun, he must perform the evening
prayer again when the Sun sets.
In the Hanafî Madhhab, only those who are on pilgrimage must perform
the two prayers one after the other (jam’) at Arafat and at Muzdalifa in Mekka.
In the Hanbalî Madhhab, it is permissible to perform two prayers one after the
other when travelling,[1] in case of illness,
for a woman when she suckles her baby and during istihâda, in case of excuses
(’udhr) that break the ablution, for those who have great difficulty in
performing ablution or tayammum or cannot know prayer times such as those who
are blind or work under the ground, and for a person whose life, property,
livelihood or chastity is in danger. For those who cannot leave their duties
for performing salât, it is not permissible to postpone it till after its
prescribed time in the Hanafî Madhhab. Only on such days, it
---------------------------------
[1] Namâz
during long-distance journeys is explained in detail in the fifteenth
chapter.
becomes permissible for
them to follow the Hanbalî Madhhab and perform early and late afternoon prayers
together or evening and night prayers together by taqdîm (performing the later
one in the time of the earlier one) or ta’khîr (performing the first one in the
time of the second). When making jam’, it is necessary to perform the early
afternoon prayer before the late afternoon prayer and the evening prayer before
the night prayer, to intend for jam’ when beginning the earlier prayer, to
perform the two prayers one right after the other, and to follow the fards and
mufsids of ablution, ghusl and salât prescribed in the Hanbalî Madhhab. Please see the last paragraph of
the twenty-second chapter!
Definition and estimation of the angle of inhitât (dip of horizon) D
for a high place has already been given on pages 130 and 142. This angle is
determined by
cos D = r/(r+Y) = 6367654/(6367654+Y) or
D=~ 0.03211 x √Y degrees
where r is the radius of the
earth, Y is the height in meters, D is the dip of horizon in degrees of angle.
The fadl-i-dair (hour angle), H can be computed in, say, degrees and
converted into hours and minutes as reckoned from midday (nisf-un-nehâr), using
a scientific calculator. The operations on a solar Privilege calculator are as
follows
H Sin - φ
sin x δ sin = ÷ φ cos
÷ δ cos
Arc cos ÷ 15 = ◦ﻭﻭﻭ→
where h is the angular altitude of the Sun during
the night,
φ is the
latitude of the location and δ is the
declination of the Sun taken (-) if in the southern hemisphere.
The adhânî time of imsâk (in hours)= 12 + Zuhr - H - (1 ÷ 3). The time
of ’ishâ’ (in hours) = H + Zuhr - 12. Prayer times anywhere can be determined
in standard time utilizing the following operations[1] :
---------------------------------
[1] On
any day, the declination of the Sun and equation of time and, for locations
with latitude 41 °, nifs fadla, fadl-i-dâir, and prayer times can be determined easily and
rapidly by using the quadrant (Rub’-i dâ’ira), which needs no calculation,
formula or calculator. It is
H + S – T = ÷ 15 + 12 – E + N = INV ◦ﻭﻭﻭi
... (3)
on a CASIO calculator where
H = hour angle (fadl-ý
dâir), ° of angle,
S = standard meridian, °
of angle,
T = longitude of the
location, ° of angle,
E = equation of time,
hours,
N = Tamkin, hours. ◦ﻭﻭﻭ
In these operations, the variables are to be substituted in degrees for
H, S
and T and in hours for E and N.
The signs of H and N are negative in a.m. and positive in p.m.
times.
The period of Tamkin should be calculated as explained on page 130. For
any location where the latitude is less than 44° and the height, Y of the
highest place is less than
0.03211 x Y √ + 1.05 = sin ÷ φ
cos ÷
δ
cos x 3.82 = INV ◦ﻭﻭﻭi
... (4)
[In
the Mâlikî and Shâfi'î Madhhabs, during a long-distance journey and/or in case of
illness and/or old age, early and late afternoon prayers, as well as evening
and night prayers, may be performed in (a convenience termed) jem', which means to perform
each pair in sucession at the time of one or the other making up the pair. (In
other words, a Muslim in one of the aforesaid two Madhhabs and undergoing one
or all the ,abovementioned three limiting situations is permitted to perform
early and late afternoon prayers in succession within the time allotted to
either, and/or to perform evening and night prayers likewise. This, however,
should not be vitiated by also joining the two pairs. Nor should one
indulge oneself into the eclecticity that all five daily prayers can be
performed in succession in the name of enjoying the convenience offered
by the aforesaid two Madhabs.)].
---------------------------------
.manufactured
and distributed along with an instructions manual by Hakîkat Kitabevi in
A computer programme can be developed which
calculates the prayer times and which can be saved on a magnetic disk, and
taken out of the computer and stored for years. The programme on the disk can
be run on a compatible computer; if the longitude and latitude of a location
are given, the prayer times for any given day or month or year can be computed
within seconds and displayed on the screen of the monitor or printed as a list
on paper. This list can be sent within seconds by fax coupled to a phone to the
city where it is required.
WARNING: It is harâm to perform
salâts before or after their due times. The time of a salât begins when the
relevant edge of the Sun comes to the altitude peculiar to that salât. There
are three reasons why the prayer times given by some calendars are different
from those given by the calendar published by the daily newspaper Türkiye:
1- They take the altitudes with respect to true horizon, whereas the
altitudes should be reckoned from the apparent line of horizon, that is, the
shar’î horizon.
2- The place of the line of apparent horizon of a location changes with
the altitude of the location. They convert the times they have determined in
accordance to the true horizon to the apparent times calculated in accordance
to the altitudes that are taken as per the apparent horizons of the lower
points of that location. Therefore, the times thus found are different from the
shar’î ones and are disputable. However, they should be converted to the times
of the highest place of the location , that is, to the canonical times based on
the canonical horizon.
3- They calculate the time when the Sun’s centre reaches the true
altitudes, whereas the time when its relevant edge reaches those altitudes
should be calculated, and the true times found thereby should be converted to
the canonical times. The Muslim ’ulamâ have introduced the concept of Tamkin to
correct these three errors. The time period of Tamkin is ten minutes for
Istanbul. Tamkin time is a shield to protect the prayers and fasts against
being fâsid (invalid). One single tamkîn is used to convert the calculated true
times of all the prayers of namâz to their calculated canonical times. There
are not different tamkîns for different prayers of namâz.